| Enoncé et corrigé en Postscript | Réponses intégrées ou à la demande |
Examen de majeure 2 Langages et compilation (Durée 2h) 29 mars 1999 |
On attachera une importance particulière à la clarté, à la précision et la la concision de la rédaction.
|
carré suivante:
|
function carré (n : integer) : integer; begin carré := n * n end; |
|
carre: mul $v0, $a0, $a0 # v0 <- n n j $ra # Retour à l'appelant |
|
carre: mul $v0, $a0, $a0 # v0 <- n n j $ra # Retour à l'appelant |
cube suivante:
|
function cube (n : integer) : integer; begin cube := carré(n) * n end; |
|
cube_f=8 cube: subu $sp, $sp, cube_f # ajustement de la pile sw $ra, 0($sp) # sauvegarde de l'adresse de retour sw $a0, 4($sp) # sauvegarde de n jal carre # v0 <- carré(n) lw $a0, 4($sp) # a0 <- n mul $v0, $a0, $v0 # v0 <- carré(n) * n lw $ra, 0($sp) # rappel de l'adresse de retour addu $sp, $sp, cube_f # ajustement de la pile j $ra |
carré dans la fonction
cube.
|
function cube (n : integer) : integer; begin cube := (n * n) * n end; |
|
cube: mul $v0, $a0, $a0 # v0 <- n * n mul $v0, $v0, $a0 # v0 <- (n * n) * n j $ra # retour à l'appelant |
carré pendant la compilation de la fonction
cube (il suffit de compiler carré avant
cube).
On saura alors, par exemple, que les registres temporaires
t0, t1, ... ne sont pas utilisés par la fonction carré
et peuvent l'être par la fonction cube pour sauvegarder les valeurs
intermédiaires et l'adresse de retour, ce qui évitera tous les mouvements de
pile dans la fonction cube.|
function quatre (n : integer) : integer; begin quatre := carré (carré (n*n)) end; |
|
function quatre (n : integer) : integer; begin quatre := ((n * n) * (n * n)) * ((n * n) * (n * n)) end; |
carré (par exemple (n*n) mais aussi
carré (n*n)) est évalué deux fois (au toral (n*n) est évalué
quatre fois) ce qui est inefficace.
|
function trace (n : integer) : integer; begin write (x); trace := x end; function erronée () : integer; begin erronée := carré (trace x) end; |
erronée évalue trace x une seule fois.
Après l'expansion en ligne naïve, trace x sera évalué deux fois
et imprimera deux fois la valeur de x, changeant ainsi
la sémantique du programme.
carré dans
la fonction quatre qui suggère un schéma général et correct.
|
function quatre (n : integer) : integer; var n1 : integer; var carré1 : integer; var n2 : integer; var carré2 : integer; begin n1 := n; (* argument de l'appel le plus interne *) carré1 := n1 * n1; (* résultat du premier appel *) n2 := carré1; (* argument du deuxième appel *) carré2 := n2 * n2; (* argument de l'appel externe *) quatre := carré2 end; |
|
|
|
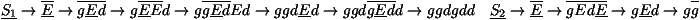
| S1 ® E ® |
ì í î |
|
S1 ® E ® e |
| a | b | first (b) | follow (a) | a ® *e | g | d |
| S | E | g | g | yes | Ö | |
| E | g E d E | g | d | yes | Ö | |
| e | Ö |
|
type g1 = G1_S of e1 and e1 = G1_gEd of e1 | G1_EE of e1 * e1 | G1_0;; |
g2 représentant les arbres
syntaxiques de la grammaire G2.
|
type g2 = G2_S of e2 and e2 = | G2_gEdE of e2 * e2 | G2_0;; |
a2
correspondant à la dérivation de ggdgdd dans G2 que vous avez donnée
ci-dessus.
|
let a2 = G2_S (G2_gEdE (G2_gEdE (G2_0, G2_gEdE (G2_0, G2_0)), G2_0));; |
mot1 qui prend
un arbre syntaxique de type g1 et qui retourne le mot (chaîne de
caractères) du langage L lui correspondant.
|
let rec lemot1 = function | G1_gEd e -> "g" ^ (lemot1 e) ^ "d" | G1_EE (e, e') -> (lemot1 e) ^ (lemot1 e') | G1_0 -> "" let mot1 (G1_S e) = lemot1 e;; |
réécrit qui transforme un arbre syntaxique a1 de type
g1 en un arbre syntaxique a2 de type g2
tel que a2 représente le même mot que a1
(la preuve de correction n'est pas demandée dans cette question).
|
let rec réécrit_le = function G1_EE (G1_EE (e, e'), e'') -> réécrit_le (G1_EE (e, G1_EE (e', e''))) | G1_EE (G1_gEd e, e') -> G2_gEdE (réécrit_le e, réécrit_le e') | G1_EE (G1_0, e) -> réécrit_le e | G1_gEd e -> G2_gEdE (réécrit_le e, G2_0) | G1_0 -> G2_0;; let réécrit (G1_S e) = G2_S (réécrit_le e);; |
réécrit est récursive.
Cependant l'argument de chaque appel récursif est un
sous-arbre strict de l'argument de l'appel principal,
sauf dans le premier cas du
filtrage: l'argument de l'appel principal est alors un noeud de la forme
G1_EE(u,v) et l'argument de l'appel récursif
est un noeud de même forme G1_EE(u',v') tel que u' soit un
sous-arbre strict de u. On ne peut donc passer par le premier cas de
filtrage qu'un nombre fini de fois; ensuite l'argument de l'appel récursif
ne peut que décroître strictement.
réécrit.
En déduire que G2 reconnaît tout L.
mot1 est égale à la composée de
mot2 (définie de façon analogue à mot1) et de réécrit.
Tout mot w de L peut être reconnu par G1 (par définition de L). Il
existe donc un arbre syntaxique a1 dont w est l'image par mot1.
L'image de a1 par la fonction réécrit est un arbre a2 de la
grammaire G2 dont l'image par mot2 est le même mot w.
Le mot w est donc aussi reconnu par G2.This document was translated from LATEX by HEVEA.