Chapitre 1  Listes

• Structure dynamique, structure séquentielle
• Listes chaînées, révisions
• Tri des listes
• Programmation objet
• Complément : listes bouclées

1.1  Structure dynamique, structure séquentielle

Les structures de données en algorithmique sont souvent complexes et de taille variable. Elles sont souvent aussi dynamiques, au sens où elles évoluent en forme et en taille en cours d’exécution d’un programme. Les listes sont l’exemple le plus simple d’une telle structure dynamique.

L’aspect dynamique renvoie aussi à la façon dont la mémoire nécessaire est allouée, la mémoire peut être allouée dynamiquement lors de l’exécution du programme, ou statiquement avant l’exécution du programme. L’allocation statique suppose que le compilateur arrive à connaître la taille de mémoire à allouer (c’est-a-dire à demander au système d’exploitation), cette taille est ensuite rangée dans le fichier exécutable produit et c’est le système d’exploitation qui alloue la mémoire demandée au moment de lancer le programme. En Pascal par exemple, la taille des tableaux globaux est donnée par des constantes, de sorte les tableaux globaux peuvent être et sont alloués statiquement.

L’allocation dynamique de la mémoire existe aussi en Pascal (il existe une fonction new), mais elle est plus délicate qu’en Java, car en Pascal, comme dans beaucoup de langages, le programmeur doit rendre explicitement les cellules de mémoire dont il n’a plus besoin au système d’exploitation. En revanche, le système d’exécution de Java est assez malin pour réaliser cette opération tout seul, ce qui permet de privilégier l’allocation dynamique de la mémoire, qui est bien plus souple que l’allocation statique.

En Java toutes les structures de données sont allouées dynamiquement — généralement par new, mais les chaînes sont également allouées dynamiquement. Il n’en reste pas moins que les tableaux manquent un peu de souplesse, puisque leur taille est fixée au moment de la création. Ainsi, un tableau n’est pas très commode pour stocker une suite de points entrés à la souris et terminée par un double clic. Il faut d’abord allouer un tableau de points à une taille par défaut N supposée suffisante et ensuite gérer le cas où l’utilisateur entre plus de N points, par exemple en allouant un nouveau tableau plus grand dans lequel on recopie les points déjà stockés. Il est bien plus commode d’organiser ces points comme une suite de petits blocs de mémoire, un bloc contenant un point et un lien vers le bloc suivant. On alloue alors la mémoire proportionnellement au nombre de points stockés sans se poser de questions. Nous avons redécouvert la liste (simplement chaînée). Une liste L⟨E⟩ de E est :

1. la liste vide,
2. ou une paire (une cellule) qui contient un élément E et la liste des éléments suivants.

Il s’agit d’une définition par induction, dans le cas 2 le mot « liste » apparaît à nouveau. On peut, sans vraiment tout expliquer, dire que l’ensemble L⟨E⟩ est décrit par l’équation suivante.

Où ∅ est la liste vide.

On notera que la définition théorique des listes ne fait plus usage du mot lien. Mais dès que l’on implémente les listes, le « lien » revient nécessairement. En Java, une liste est une référence (voir B.3.1.1), qui est :

1. soit la référence null qui ne pointe nulle part et représente la liste vide,
2. ou bien une référence qui pointe vers une cellule contenant un élément et une liste.

Autrement dit voici une définition possible des cellules de liste de points en Java.

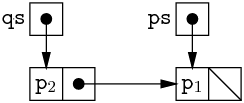
La cellule de liste est donc un objet de la classe PointList et une valeur de type PointList est bien une référence, puisque les valeurs des objets sont des références. On peut comprendre un aspect de l’organisation des listes à l’aide de dessins qui décrivent une abstraction de l’état de la mémoire, c’est-à-dire une simplification de cet état, sans les détails techniques. Par exemple, on suppose donnés deux points p1 et p2, et on produit les listes :

Alors, l’état final de la mémoire est schématisé ainsi :

Étant entendu que, dans ce type de schéma, les flèches représentent les références, la barre diagonale null, les boîtes nommées les variables, et les boîtes anonymes les cellules mémoire allouées par new (voir B.3.1).

Il semble que ce qu’est une liste dans la vie de tous les jours est clair : une liste est une séquence d’éléments. Par exemple la liste des admis à un concours quelconque, ou la liste de courses que l’on emporte au supermarché pour ne rien oublier. L’intuition est juste, elle fait en particulier apparaître (surtout dans le premier exemple) que l’ordre des éléments d’une liste importe. Mais méfions nous un peu, car la liste de l’informatique est très contrainte. En effet, les opérations élémentaires possibles sur une liste ℓ sont peu nombreuses :

1. Tester si une liste est la liste vide ou pas (ℓ == null),
2. et si ℓ est (une référence vers) une cellule (e, ℓ′), on peut
   1. extraire le premier élément e (ℓ.val),
   2. ou bien extraire la liste qui suit ℓ (ℓ.next).

Pour construite les listes, il n’y a que deux opérations,

1. la liste vide existe (null),
2. on peut ajouter un nouvel élément e en tête d’une liste ℓ (new PointList(e, ℓ)).

Et c’est tout, toutes les autres opérations doivent être programmées à partir des opérations élémentaires.

Une opération fréquemment programmée est le parcours de tous les éléments d’une liste. Cette opération se fait idéalement selon un idiome, c’est-à-dire selon une tournure fréquemment employée qui signale l’intention du programmeur, ici une boucle for.

Les programmeurs Java emploient normalement une telle boucle pour signaler que leur code réalise un simple parcours de liste. Dès lors, la lecture de leur code en est facilitée. Notons que rien, à part le souci de la coutume, ne nous empêche d’employer un autre type de boucle, par exemple

La liste simplement chaînée est une structure séquentielle. Une structure séquentielle regroupe des éléments en séquence et l’accès à un élément donné ne peut se faire qu’en parcourant la structure, jusqu’à trouver l’élément cherché. Cette technique d’accès séquentiel s’oppose à l’accès direct. Un exemple simple de structure de données qui offre l’accès direct est le tableau. La distinction entre séquentiel et direct se retrouve dans des dispositifs matériels : une bande magnétique n’offre qu’un accès séquentiel puisqu’il faut dérouler toute la bande pour en lire la fin ; en revanche la mémoire de l’ordinateur offre l’accès direct. En effet, on peut voir la mémoire comme un grand tableau (d’octets) dont les indices sont appelés adresses. L’accès au contenu d’une case se fait simplement en donnant son adresse. En fait le tableau est une abstraction de la mémoire de l’ordinateur.

En résumé la liste est une structure dynamique, parce que la mémoire est allouée petit à petit directement en fonction des besoins. La liste peut être définie inductivement, ce qui rend la programmation récursive assez naturelle (inductif et récursif sont pour nous informaticiens des synonymes). Enfin, par nature, la liste est une structure de données séquentielle, et le parcours de la structure est privilégié par rapport à l’accès à un élément arbitraire.

1.2  Listes chaînées, révisions

Les listes chaînées ont déjà été vues dans le cours précédent. Nous commençons donc par quelques révisions. Attention, nous profitons de ce que les listes ont « déjà été vues en cours » pour systématiser les techniques de programmation sur les listes. Il y a sans doute un vrai profit à lire cette section. Si vous en doutez, essayez tout de suite les exercices de la section 1.2.4.

1.2.1  Opérations élémentaires sur les listes

Comme révision nous montrons comment réaliser les ensembles (d’entiers) à partir des listes (d’entiers). Voici la définition des cellules de liste d’entiers.

Un ensemble est représenté par une liste dont tous les éléments sont deux à deux distincts. Nous ne spécifions aucune autre contrainte, en particulier aucun ordre des éléments d’une liste n’est imposé. Pour la programmation, un premier point très important à prendre en compte est que null est un ensemble valable. Il est alors naturel d’écrire des méthodes statiques, car null qui ne possède aucune méthode est une valeur légitime pour une variable de type List.

Commençons par calculer le cardinal d’en ensemble. Compte tenu de ce que les éléments des listes sont deux à deux distincts, il suffit de calculer la longueur d’une liste. Employons donc la boucle idiomatique

Ce premier code fait apparaître qu’il n’est pas toujours utile de réserver une variable locale pour la boucle idiomatique. Écrire xs = xs.next ne fait que changer la valeur de la variable locale xs (qui appartient en propre à l’appel de méthode) et n’a pas d’impact sur la liste elle-même. Ainsi écrire le code suivant ne pose pas de problème particulier.

À la fin du code, la variable xs existe toujours et référence toujours la première cellule de la liste {1, 2, 3, 4}. En fait, cette variable xs n’a rien à voir avec le paramètre homonyme de la méthode card et heureusement.

Poursuivons en affichant les ensembles, ou, plus exactement, en fabriquant une représentation affichable des ensembles sous forme de chaîne. Voici un premier essai d’écriture d’une méthode statique toString dans la classe List avec la boucle idiomatique.

Le code est critiquable :

• L’affichage est laid, il y a une virgule en trop à la fin. Par exemple, pour la liste des entiers 1 et 3, on obtient "{1, 3, }".
• Le coût de production de la chaîne est quadratique en la longueur de la liste. En effet la concaténation de deux chaînes (par +) coûte en proportion de la somme des longueurs des chaînes concaténées, car il faut allouer une nouvelle chaîne pour y recopier les caractères des chaînes concaténées. Pour une liste xs de longueur n on procède donc à n concaténations de chaînes, de tailles supposées régulièrement croissantes ce qui mène au final à un coût quadratique.

  k + 2 × k + ⋯ n × k =

  n(n+1) 2

  k

Pour remédier au premier problème on peut distinguer le cas du premier élément de la liste. Pour remédier au second problème il faut utiliser un objet StringBuilder de la bibliothèque Java (voir B.6.1.4). Les objets StringBuilder sont des chaînes dynamiques, dont on peut changer la taille. En particulier, ils possèdent une méthode append(String str) qui permet de leur ajouter une chaîne str à la fin, pour un coût que l’on peut considérer proportionnel à la longueur de str. Bref on a :

Après cet échauffement, écrivons ensuite la méthode mem qui teste l’appartenance d’un entier à un ensemble.

On emploie la boucle idiomatique, afin de parcourir la liste et de retourner de la méthode mem dès qu’un entier égal à x est trouvé. Comme on le sait certainement déjà une écriture récursive est également possible.

La version récursive provient directement de la définition inductive des listes, elle tient en deux équations :

Ces deux équations sont le support d’une preuve par induction structurelle évidente de la correction de mem.

Alors, que choisir ? De façon générale le code itératif (le premier, avec une boucle) est plus efficace que le code récursif (le second), ne serait-ce que parce que les appels de méthode sont assez coûteux. Mais le code récursif résulte d’une analyse systématique de la structure de données inductive, et il a bien plus de chances d’être juste du premier coup. Ici, dans un cas aussi simple, le code itératif est préférable (en Java qui favorise ce style).

1.2.2  Programmation sûre, style dit fonctionnel

Nous envisageons maintenant des méthodes qui fabriquent de nouveaux ensembles. Commençons par la méthode add qui ajoute un élément à un ensemble. Le point remarquable est qu’un ensemble contient au plus une fois un élément donné. Une fois disponible la méthode mem, écrire add est très facile.

Attaquons ensuite la méthode remove qui enlève un élément x d’un ensemble X. Nous choisissons de suivre le principe des structures de données dites fonctionnelles ou non-mutables ou encore persistantes. Selon ce principe, on ne modifie jamais le contenu des cellules de liste. Cela revient à considérer les listes comme définies inductivement par L⟨E⟩ = {∅} ∪ (E × L⟨E⟩), et il est important d’admettre dès maintenant que cette approche rend la programmation bien plus sûre.

Pour écrire remove, raisonnons inductivement : dans un ensemble vide, il n’y a rien à enlever ; tandis que dans un ensemble (une liste) X = (x′, X′) on distingue deux cas :

• L’élément x à enlever est égal à x′ et alors X moins x est X′, car X est une liste d’éléments deux à deux distincts et donc X′ ne contient pas x.
• Sinon, il faut enlever x de X′ et ajouter x′ à la liste obtenue, dont on sait qu’elle ne peut pas contenir x′.

Soit en équations :

Et en Java :

En ce qui concerne l’état mémoire, remove(x,xs) renvoie une nouvelle liste (il y a des new), dont le début est une copie du début de xs, jusqu’à trouver l’élément x. Plus précisément, si nous écrivons

Alors on a les structures suivantes en mémoire

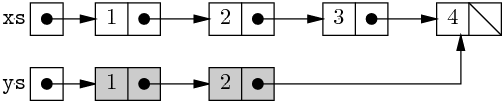
(Les cellules allouées par remove sont grisées.) On constate que la partie de la liste xs qui précède l’élément supprimé est recopiée, tandis que la partie qui suit l’élément supprimé est partagée entre les deux listes. Dans le style persistant on en vient toujours à copier les parties des structures qui sont changées.

Au passage, si on écrit plutôt

Alors on obtient

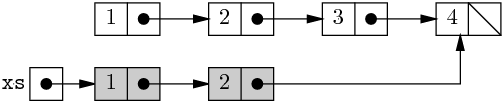
C’est-à-dire exactement la même chose, sauf que la variable xs pointe maintenant vers la nouvelle liste et qu’il n’y a plus de référence vers la première cellule de l’ancienne liste. Il en résulte que la mémoire occupée par les trois premières cellules de l’ancienne liste ne peut plus être accédée par le programme. Ces cellules sont devenues les miettes et le gestionnaire de mémoire de l’environnement d’exécution de Java peut les récupérer. Le ramassage des miettes (garbage collection) est automatique en Java, et c’est un des points forts du langage.

Écrivons maintenant remove avec une boucle. Voici un premier essai : parcourir la liste xs en la recopiant en évitant de copier tout élément égal à x.

Et ici apparaît une différence, alors que la version récursive de remove préserve l’ordre des éléments de la liste, la version itérative inverse cet ordre. Pour s’en convaincre, on peut remarquer que lorsque qu’une nouvelle cellule new List(xs.val, r) est construite, l’élément xs.val est ajouté au début de la liste r, tandis qu’il est extrait de la fin de la liste des éléments déjà parcourus. On peut aussi schématiser l’état mémoire sur l’exemple déjà utilisé. 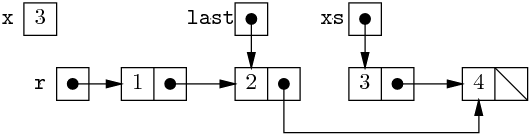Avant la boucle on a

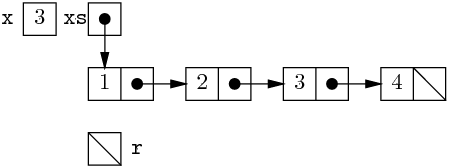
La figure 1.1 schématise l’état de la mémoire à la fin de chacune des quatre itérations, la cellule nouvelle étant grisée.

---

Figure 1.1: Les quatre itérations de remove

---

Et enfin voici le bilan de l’état mémoire, pour le programme complet.

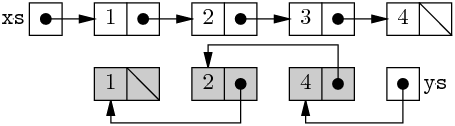
L’inversion n’a pas d’importance ici, puisque les ensembles sont des listes d’éléments deux à deux distincts sans autre contrainte, le code itératif convient. Il n’en y irait pas de même si les listes étaient ordonnées.

Il est possible de procéder itérativement et de conserver l’ordre des éléments. Mais c’est un peu plus difficile. On emploie une technique de programmation que faute de mieux nous appellerons initialisation différée. Jusqu’ici nous avons toujours appelé le constructeur des listes à deux arguments, ce qui nous garantit une bonne initialisation des champs val et next des cellules de liste. Nous nous donnons un nouveau constructeur List (int val) qui initialise seulement le champ val.¹ Le champ next sera affecté une seule fois plus tard, ce qui revient moralement à une initialisation.

Pour illustrer l’initialisation différée, nous commençons par un exemple plus facile.

Solution. L’idée revient à parcourir la liste xs en copiant ses cellules et en délégant l’initialisation du champ next à l’itération suivante. Il y a un petit décalage à gérer au début et à la fin du parcours.

static List copy(List xs) {
  if (xs == null) return null ;
  // Ici la copie possède au moins une cellule, que voici
  List r = new List (xs.val) ;
  // last pointe sur la dernière cellule de la liste r
  List last = r ;
  // Parcourir la suite de xs
  for ( xs = xs.next ; xs != null ; xs = xs.next ) {
    // « initialiser » last.next à une nouvelle cellule
    last.next = new List (xs.val) ;
    /** qui devient donc la dernière cellule du résultat **/
    last = last.next ;
  }
 // « initialiser » le next de la toute dernière cellule à une liste vide
  last.next = null ; // Inutile, mais c'est plus propre
  return r ;
}

On observe que le code construit une liste sur laquelle il maintient deux références, r pointe sur la première cellule, tandis que last pointe sur la dernière cellule — sauf très brièvement au niveau du commentaire /**…**/, où last pointe sur l’avant-dernière cellule. Plus précisément, la situation en « régime permanent » avant la ligne qui précède le commentaire /**…**/ est la suivante :

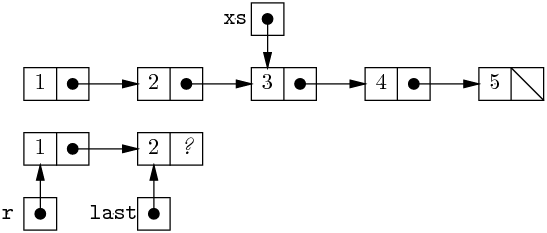
Et après ajout d’une nouvelle cellule par last.next = new List(xs.val).

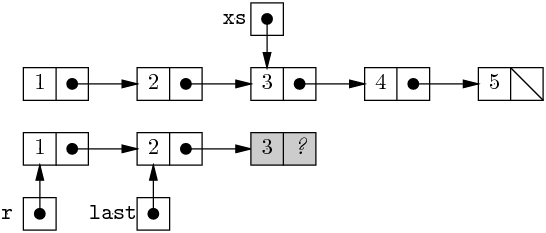
(La cellule qui vient d’être allouée est grisée). Et enfin après exécution de l’affectation last == last.next.

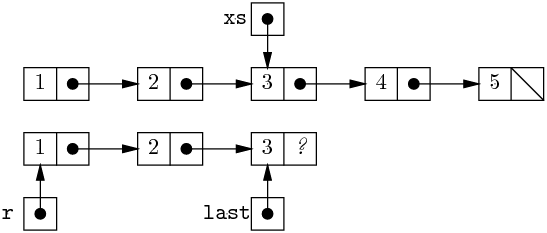
On conçoit qu’avec un tel dispositif il est facile d’ajouter de nouvelles cellules de liste à la fin du résultat et possible de rendre le résultat (avec r qui pointe sur la première cellule). On observe le cas particulier traité au début, il résulte de la nécessité d’identifier le cas où il ne faut pas construire la première cellule du résultat.

Enfin, la méthode itérative construit exactement la même liste que la méthode récursive, même si les cellules de listes sont allouées en ordre inverse. En effet la méthode récursive alloue la cellule après que la valeur du champ next est connue, tandis que la méthode itérative l’alloue avant. □

La figure 1.2 donne la nouvelle version itérative de remove, écrite selon le principe de l’initialisation différée. Par rapport à la copie de liste, le principal changement est la possibilité d’arrêt de la copie à l’intérieur de la boucle.

---

Figure 1.2: Enlever un élément selon la technique de l’initialisation différée

static List remove(int x, List xs) {
  /* Deux cas particuliers */
  if (xs == null) return null ;
  /* Ici xs != null, donc xs.val existe */
  if (x == xs.val) return xs.next ;
  /* Ici la première cellule du résultat existe et contient xs.val */
  List r = new List (xs.val) ;
  List last = r ;
  /* Cas général : copier xs (dans r), jusqu'à trouver x */
  for ( xs = xs.next ; xs != null ; xs = xs.next ) {
    if (x == xs.val) {
      // « initialiser » last.next à xs moins xs.val (c-a-d. xs.next)
      last.next = xs.next ;
      return r ;
    }
    // « initialiser » last.next à une nouvelle cellule
    last.next = new List (xs.val) ;
    last = last.next ;
  }
  // « initialiser » last.next à une liste vide
  last.next = null ;  // Inutile mais c'est plus propre.
  return r ;
}

---

En effet, lorsque l’élément à supprimer est identifié (x == xs.val), nous connaissons la valeur à ranger dans last.next, puisque par l’hypothèse « xs est un ensemble », xs moins l’élément x est exactement xs.next, on peut donc arrêter la copie. On observe également les deux cas particuliers traités au début, ils résultent, comme dans la copie de liste, de la nécessité d’identifier les cas où il ne faut pas construire la première cellule du résultat. Au final le code itératif est quand même plus complexe que le code récursif. Par conséquent, si l’efficacité importe peu, par exemple si les listes sont de petite taille, la programmation récursive est préférable.

Nous pouvons maintenant étendre les opérations élémentaires impliquant un élément et un ensemble et programmer les opérations ensemblistes du test d’inclusion, de l’union et de la différence. Pour programmer le test d’inclusion xs ⊆ ys, il suffit de tester l’appartenance de tous les éléments de xs à ys.

1.2.3  Programmation dangereuse, structures mutables

Les méthodes remove de la section précédente copient tout ou partie des cellules de la liste passée en argument. On peut, par exemple dans un souci (souvent mal venu, disons le tout de suite) d’économie de la mémoire, chercher à éviter ces copies. C’est parfaitement possible, à condition de s’autoriser les affectations des champs des cellules de liste. On parle alors de structure de données mutable ou impérative. Ainsi, dans le remove récursif on remplace l’allocation d’une nouvelle cellule par la modification de l’ancienne cellule, et on obtient la méthode nremove destructive ou en place suivante

On peut adapter la seconde version itérative de remove (figure 1.2) selon le même esprit, les références r et last pointant maintenant, non plus sur une copie de la liste passée en argument, mais sur cette liste elle-même.

On note que la version itérative comporte des affectations de last.next inutiles. En effet, à l’intérieur de la boucle les références xs et last.next sont toujours égales, car last pointe toujours sur la cellule qui précède xs dans la liste passée en argument, sauf très brièvement au niveau du second commentaire /**…**/. En régime permanent, la situation au début d’une itération de boucle (avant le premier commentaire /**…**/) est la suivante

Et en fin d’itération, après le second commentaire /**…**/, on a

Au début de l’itération suivante on a

La recherche de xs.val == x est terminée, et le champ next de la cellule last qui précède la cellule xs est affecté.

Puis la liste r est renvoyée.

Au final, l’effet de nremove(int x, List xs) s’apparente à un court-circuit de la cellule qui contient x. Ainsi exécuter

produit l’état mémoire

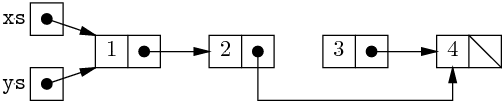
Un problème majeur survient donc : l’ensemble xs est modifié ! On comprend donc pourquoi nremove est dite destructive. On peut se dire que cela n’est pas si grave et que l’on saura en tenir compte. Mais c’est assez vain, car si on supprime le premier élément de l’ensemble xs, le comportement est différent

Alors on obtient

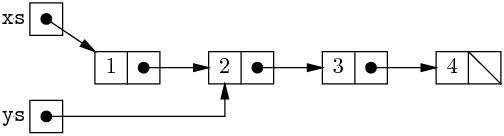
Et on observe qu’alors l’ensemble xs n’a pas changé.

En conclusion, la programmation des structures mutables est tellement délicate qu’il est souvent plus raisonnable de s’abstenir de l’employer. Comme toujours en programmation, la maxime ci-dessus souffre des exceptions, dans les quelques cas où l’on possède une maîtrise complète des structures de données, et en particulier, quand on est absolument sûr que les structures modifiées ne sont connues d’aucune autre partie du programme.

Un bon exemple de ce type d’exception est la technique d’initialisation différée employée dans la seconde méthode remove itérative de la figure 1.2. En effet, le champ next est affecté une seule fois, et seulement sur des cellules fraîches, allouées par la méthode remove elle-même, et qui ne sont accessible qu’à partir des variables r et last elles-mêmes locales à remove. Par conséquent, les modifications apportées à certaines cellules sont invisibles de l’extérieur de remove.

1.2.4  Contrôle de la révision

Nous avons divisé les techniques de programmation sur les listes selon deux fois deux catégories. Les listes peuvent être fonctionnelles (persistantes) ou mutables (impératives), et la programmation peut être récursive ou itérative.

Afin d’être bien sûr d’avoir tout compris, programmons une opération classique sur les listes des quatre façons possibles. Concaténer deux listes signifie, comme pour les chaînes, ajouter les éléments d’une liste à la fin de l’autre. Nommons append la méthode qui concatène deux listes. La programmation récursive non-mutable résulte d’une analyse simple de la structure inductive de liste.

Nommons nappend la version mutable de la concaténation. L’écriture récursive de nappend à partir de la version fonctionnelle est mécanique. Il suffit de remplacer les allocations de cellules par des modifications.

Pour la programmation itérative non-mutable, on a recours à l’initialisation différée.

Pour la programmation mutable et itérative, on supprime les allocations de la version non-mutable et on remplace les initialisations différées par des affectations des champs next de la liste passée comme premier argument. On n’explicite que la dernière affectation de last.next qui est la seule qui change quelque chose.

Voici un autre codage plus concis de la même méthode, qui met en valeur la recherche de la dernière cellule de la liste xs.

Enfin on constate que le coût de la concaténation est de l’ordre de n opérations élémentaires, où n est la longueur de la première liste.

Solution. Le programme affecte la référence xs au champ next de la dernière cellule de la liste xs. Il en résulte une liste « bouclée ».

□

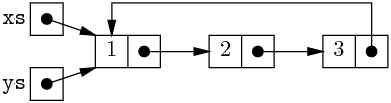
Et pour être vraiment sûr d’avoir compris, nous conseillons encore un exercice, d’ailleurs un peu piégé.

1.3  Tri des listes

Nous disposons désormais de techniques de programmation élémentaires sur les listes. Il est temps d’aborder des programmes un peu plus audacieux, et notamment de considérer des algorithmes. Le tri est une opération fréquemment effectuée. En particulier, les tris interviennent souvent dans d’autres algorithmes, dans le cas fréquent où il plus simple ou plus efficace d’effectuer des traitements sur des données prises dans l’ordre plutôt que dans le désordre.

Les algorithmes de tri sont nombreux et ils ont fait l’objet d’analyses très fouillées, en raison de leur intérêt et de leur relative simplicité. Sur ce point [6] est une référence fondamentale.

1.3.1  Tri par insertion

Ce tri est un des tris de listes les plus naturels. L’algorithme est simple : pour trier la liste xs, on la parcourt en insérant ses éléments à leur place dans une liste résultat qui est donc triée. C’est la technique généralement employée pour trier une main dans les jeux de cartes.

Il reste à écrire l’insertion dans une liste triée. L’analyse inductive conduit à la question suivante : soit x un entier et Y une liste triée, quand la liste (x,Y) est elle triée ? De toute évidence cela est vrai, si

• Y est la liste vide ∅,
• ou bien, Y = (y, Y′) et x ≤ y.

En effet, si x ≤ y, alors tous les éléments de Y triée sont plus grands (au sens large) que x, par transitivité de ≤. Notons P(X) le prédicat défini par

Soit I fonction d’insertion, selon l’analyse précédente on pose

Si P(x, Y) est invalide, alors Y s’écrit nécessairement Y = (y, Y′) et on est tenté de poser

Et on aura raison. On montre d’abord (par induction structurelle) le lemme évident que I(x, Y) regroupe les éléments de Y plus x. Ensuite on montre par induction structurelle que I(x,Y) est triée.

Base

Si P(x,Y) est vrai (ce qui comprend le cas Y = ∅), alors I(x,Y) est triée.

Induction

Sinon, on a Y = (y, Y′). Par hypothèse d’induction I(x, Y′) est triée. Par ailleurs, les éléments de I(x, Y′) sont ceux de Y′ plus x, et donc y est plus petit (au sens large) que tous les éléments de I(x, Y′) (par hypothèse (y,Y′) triée et P(x,Y) invalide). Soit finalement (y,I(x, Y′)) est triée.

Il reste à programmer d’abord le prédicat P,

puis la méthode d’insertion insert.

Penchons nous maintenant sur le coût de notre implémentation du tri par insertion. Par coût nous entendons d’abord temps d’exécution. Les constructions élémentaires de Java employées² s’exécutent en temps constant c’est à dire que leur coût est borné par une constante. Il en résulte que même si le coût d’un appel à la méthode here est variable, selon que le paramètre ys vaut null ou pas, ce coût reste inférieur à une constante correspondant à la somme des coûts d’un appel de méthode à deux paramètres, d’un test contre null, d’un accès au champs val etc.

Il n’en va pas de même de la méthode insert qui est récursive. De fait, le coût d’un appel à insert s’exprime comme une suite I(n) d’une grandeur qui exprime la taille de l’entrée, ici la longueur de la liste ys.

Notons que pour borner I(n+1) nous avons supposé qu’un appel récursif était effectué. Il est donc immédiat que I(n) est majorée par k₁·n + k₀. En première approximation, la valeur des constantes k₁ et k₀ importe peu et on en déduit l’information pertinente que I(n) est en O(n).

En regroupant le coût des diverses instructions de coût constant de la méthode insertionSort selon qu’elles sont exécutées une ou n fois, et en tenant compte des n appels à insert, le coût S(n) d’un appel de cette méthode est borné ainsi :

Et donc le coût de insertionSort est en O(n²). Il s’agit d’un coût dans le cas le pire en raison des majorations effectuées (ici sur I(n) principalement). Notons que la notation f(n) est en O(g(n)) (il existe une constante k telle que, pour n assez grand, on a f(n) ≤ k·g(n)) est particulièrement justifiée pour les coûts dans le cas le pire. Il faut noter que l’on peut généralement limiter les calculs aux termes dominants en n. Ici on dira, insertionSort appelle n fois insert qui est en O(k) pour k ≤ n, et que insertionSort est donc en O(n²).

On peut aussi compter précisément une opération en particulier. Pour un tri on a tendance à compter les comparaisons entre éléments. La démarche se justifie de deux façons : l’opération comptée est la plus coûteuse (ici que l’on songe au tri des lignes d’un fichier par exemple), ou bien on peut affecter un compte borné d’opérations élémentaires à chacune des opérations comptées. Nous y reviendrons, mais comptons d’abord les comparaisons effectuées par un appel à insert.

On encadre ensuite facilement le nombre de comparaisons effectuées par insertionSort pour une liste de taille n+1.

Par conséquent S(n) effectue au plus de l’ordre de n² comparaisons et au moins de l’ordre de n comparaisons. « De l’ordre de » a ici le sens précis que nous avons trouvé des ordres de grandeur asymptotiques pour n tendant vers +∞. Plus exactement encore, S(n) est bornée supérieurement par une fonction en Θ(n²) et bornée inférieurement par une une fonction en Θ(n). Il est rappelé (cf. le cours précédent) que f est dans Θ(g) quand il existe deux constantes k₁ et k₂ telles que, pour n assez grand, on a

Par ailleurs, nous disposons d’une estimation réaliste du coût global. En effet, d’une part, à une comparaison effectuée dans un appel donné à insert nous associons toutes les opérations du corps de cette méthode ; et d’autre part, le coût des opérations en temps constant effectuées lors d’une itération de la boucle de insertionSort peut être affecté aux comparaisons effectuées par l’appel à insert de cette itération.

On peut pareillement estimer le coût en mémoire. Ici on peut se contenter de compter les cellules de liste allouées, et voir qu’un tri alloue au plus de l’ordre de n² cellules et au moins de l’ordre de n cellules.

1.3.2  Tri fusion

Le tri par insertion résulte essentiellement de l’opération d’insertion dans une liste triée. Un autre tri plus efficace résulte de l’opération de fusion de deux listes triés. Par définition, la fusion de deux listes triées est une liste triée qui regroupe les éléments des deux listes fusionnées. Cette opération peut être programmée efficacement, mais commençons par la programmer correctement. Sans que la programmation soit bien difficile, c’est notre premier exemple de fonction qui opère par induction sur deux listes. Soit M(X,Y) la fusion (M pour merge). Il y a deux cas à considérer

Base

De toute évidence, M(∅, Y) = Y et M(X, ∅) = X

Induction

On a X = (x,X′) et Y = (y,Y′). On distingue deux cas à peu près symétriques.

• Si x ≤ y, alors x minore non seulement tous les éléments de X′ (X est triée) mais aussi tous les éléments de Y (transitivité de ≤ et Y est triée). Procédons à l’appel récursif M(X′, Y), qui par hypothèse d’induction renvoie une liste triée regroupant les éléments de X′ et de Y. Donc, x minore tous les éléments de M(X′, Y) c’est à dire que la liste (x, M(X′, Y)), qui regroupe bien tous les éléments de X et Y, est triée. On pose donc

  M(X,Y)  = (x, M(X′, Y)),   quand X = (x,X′), Y = (y,Y′) et x ≤ y

• Sinon, alors y < x et donc y ≤ x. On raisonne comme ci-dessus, soit on pose

  M(X,Y)  = (y, M(X, Y′)),   quand X = (x,X′), Y = (y,Y′) et x > y

Et en Java, il vient

On observe que la méthode merge termine toujours, car les appels récursifs s’effectuent sur une structure plus petite que la structure passée en argument, ici une paire de listes.

Estimons le coût de la fusion de deux listes de tailles respectives n₁ et n₂, en comptant les comparaisons entre éléments. Au mieux, tous les éléments d’une des listes sont inférieurs à ceux de l’autre liste. Au pire, il y a une comparaison par élément de la liste produite.

Par ailleurs M(n₁,n₂) est une estimation raisonnable du coût global, puisque compter les comparaisons revient quasiment à compter les appels et que, hors un appel récursif, un appel donné effectue un nombre borné d’opérations toutes en coût constant.

Trier une liste xs à l’aide de la fusion est un bon exemple du principe diviser pour résoudre. On sépare d’abord xs en deux listes, que l’on trie (inductivement) puis on fusionne les deux listes. Pour séparer xs en deux listes, on peut regrouper les éléments de rangs pair et impair dans respectivement deux listes, comme procède le début du code de la méthode mergeSort.

Il reste à procéder aux appels récursifs et à la fusion, en prenant bien garde d’appeler récursivement mergeSort exclusivement sur des listes de longueur strictement plus petite que la longueur de xs.

Comptons les comparaisons qui sont toutes effectuées par la fusion :

Soit l’encadrement

Si n = 2^p+1 on a la simplification très nette

Ou encore

Les récurrences sont de la forme T(0) = 0, T(p+1) = k + T(p) de solution k·p. On a donc l’encadrement

Soit un coût de l’ordre de n logn qui se généralise à n quelconque (voir l’exercice). Le point important est que le tri fusion effectue toujours de l’ordre de n logn comparaisons d’éléments. Par ailleurs, le compte des comparaisons estime le coût global de façon réaliste, puisque que l’on peut affecter le coût de entre une et deux itérations de la boucle de séparation à chaque comparaison de la fusion.

1.3.3  Trier de grandes listes

Pour confirmer le réalisme des analyses de complexité des tris, nous trions des listes de N entiers et mesurons le temps d’exécution des deux tris par insertion I et fusion M (source List.java). Les éléments des listes sont les N premiers entiers dans le désordre.

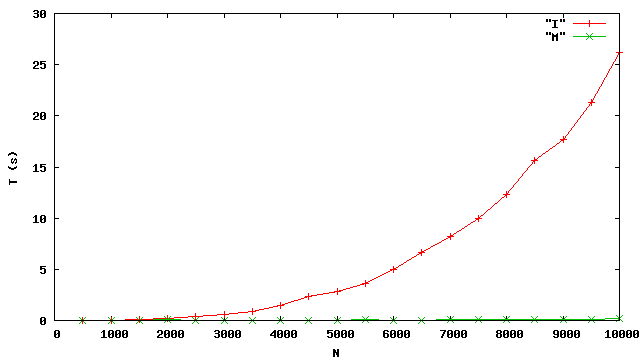
Cette expérience semble confirmer que le tri par insertion est quadratique. Elle montre surtout que le tri fusion est bien plus efficace que le tri par insertion.

Encouragés, nous essayons de mesurer le temps d’exécution du tri fusion pour des valeurs de N plus grandes. Nous obtenons :

N=10000 T=0.093999
N=20000 T=0.411111
N=30000 T=0.609787
Exception in thread "main" java.lang.StackOverflowError
        at List.merge(List.java:80)
        at List.merge(List.java:78)
  ⋮

Où de l’ordre de 1000 lignes at List.merge… sont effacées.

On voit que notre programme échoue en signalant que l’exception StackOverflowError (débordement de la pile) a été lancée. Nous expliquerons plus tard précisément ce qui se passe. Pour le moment, contentons nous d’admettre que le nombre d’appels de méthode en attente est limité. Or ici, merge appelle merge qui appelle merge qui etc. et merge doit attendre le retour de merge qui doit attendre le retour de merge qui etc. Et nous touchons là une limite de la programmation récursive. En effet, alors que nous avons programmé une méthode qui semble théoriquement capable de trier des centaines de milliers d’entiers, nous ne pouvons pas l’exécuter au delà de 30000 entiers.

Pour éviter les centaines de milliers d’appels imbriqués de merge nous pouvons reprogrammer la fusion itérativement. On emploie la technique de l’initialisation différée (voir l’exercice 1.2), puisqu’il est ici crucial de construire la liste résultat selon l’ordre des listes consommées.

La nouvelle méthode merge n’a rien de difficile à comprendre, une fois assimilée l’initialisation différée. Il faut aussi ne pas oublier d’initialiser le champ next de la toute dernière cellule allouée.

Mais attendons ! Le nouveau tri peut il fonctionner en pratique, puisque mergeSort elle même est récursive ? Oui, car mergeSort s’appelle sur des listes de longueur divisée par deux, et donc le nombre d’appels imbriqués de mergeSort vaut au plus à peu près log₂(N), certainement inférieur à 32 dans nos expériences où N est un int. Ceci illustre qu’il n’y a pas lieu de « dérécursiver » systématiquement.

Plutôt que de simplement mesurer le temps d’exécution du nouveau mergeSort, nous allons le comparer à un autre tri : celui de la bibliothèque de Java. La méthode statique sort (classe Arrays, package java.util) trie un tableau de int passé en argument. Puisque nous tenons à trier une liste, il suffit de changer cette liste en tableau, de trier le tableau, et de changer le tableau en liste.

Employer une méthode de tri de la bibliothèque est probablement une bonne idée, car elle est écrite avec beaucoup de soin et est donc très efficace [1]. Observons qu’en supposant, et c’est plus que raisonnable, un coût du tri en O(N logN), qui domine asymtotiquement nos transferts de liste en tableau et réciproquement (en O(N)), on obtient un tri en O(N logN). Dans les mesures, M est notre nouveau tri fusion, tandis que A est le tri arraySort.

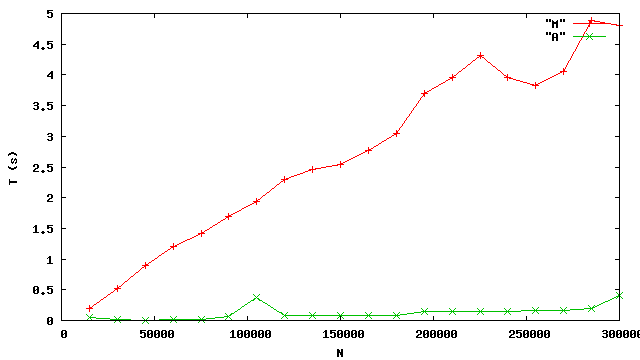
On voit que notre méthode mergeSort conduit à un temps d’exécution qui semble à peu près linéaire, mais qu’il reste des progrès à accomplir. De fait, en programmant un tri fusion destructif (voir [7, Chapitre 12] ou le code présent dans List.java par ex.) qui n’alloue aucune cellule, on obtient des temps bien meilleurs. À vrai dire, les temps sont de l’ordre du double de ceux du tri de la bibliotèque.

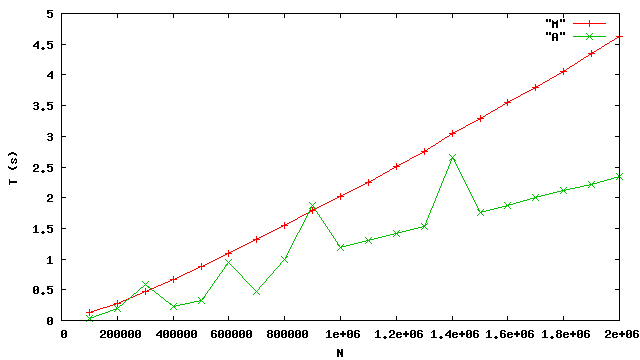
Les pics des temps du tri de bibliothèque A sont probablement dus aux interventions du gestionnaire mémoire qui sont moins discrètes que dans le cas du tri fusion en place M.

La présence de ces pics jette un doute sur la pertinence de nos mesures. voici une autre série de mesures, réalisées sur une autre machine plus rapide, disposant d’un processeur plus moderne (64 bits).

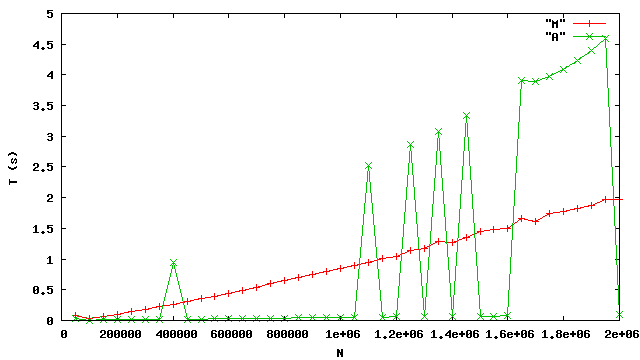
Nous constatons que la forme de la courbe M ne change pas. En revanche les irrégularités de la courbe A sont accentuées : dans le meilleur des cas, le tri de bibliothèque est bien plus performant relativement au tri fusion que dans l’expérience précédente ; tandis que dans le pire des cas, la dégradation de performance est plus marquée.

En définitive, on constate que l’analyse pratique des performances est un exercice délicat dans le cadre d’un système complet. Clairement, les détails de la courbe A dépendent significativement du gestionnaire mémoire, dont il est difficile de faire abstraction.

1.4  Programmation objet

Dans tout ce chapitre nous avons exposé la structure des listes. C’est-à-dire que les programmes qui se servent de la classe des listes le font directement, en pleine conscience qu’ils manipulent des structures de listes. Cette technique est parfaitement correcte et féconde, mais elle ne correspond pas à l’esprit d’un langage objet. Supposons par exemple que nous voulions implémenter les ensembles d’entiers. Il est alors plus conforme à l’esprit de la programmation objet de définir un objet « ensemble d’entiers » Set. Cette mise en forme « objet » n’abolit pas la distinction fondamentale des deux sortes de structures de données, mutable et non mutable, bien au contraire.

1.4.1  Ensembles non mutables

Spécifions donc une classe Set des ensembles.

Comparons la signature de méthode add des Set à celle de la méthode add de la classe List.

La nouvelle méthode add n’est plus statique, pour produire un ensemble augmenté, on utilise maintenant la notation objet : par exemple s.add(1) renvoie le nouvel ensemble s ∪ { 1} — alors que précédemment on écrivait List.add(s, 1) (voir section 1.2.2). On note que pour pouvoir appeler la méthode add sur tous les objets Set, il n’est plus possible d’encoder l’ensemble vide par null. L’ensemble vide est maintenant un objet construit par new Set ().

Bien entendu, il faut qu’une structure concrète regroupe les éléments des ensembles. Le plus simple est d’encapsuler une liste dans chaque objet Set.

La variable d’instance xs et le constructeur qui prend une liste en argument sont privés, de sorte que les clients de Set ne peuvent pas manipuler la liste cachée. Les « clients » sont les parties du programme qui appellent les méthodes de la classe Set.

Comme le montre l’exemple suivant, il importe que les listes soient traitées comme des listes non-mutables. En effet, soit le bout de programme

Nous obtenons l’état mémoire simplifié

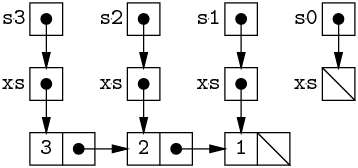
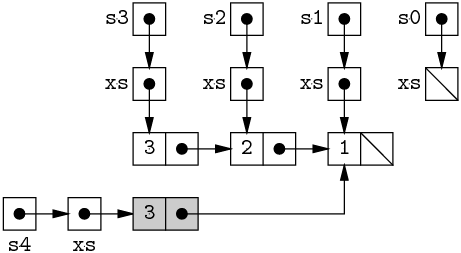
La méthode remove (section 1.2.2) ne modifie pas les champs des cellules de listes, de sorte que que le programme

n’entraîne aucune modification des ensembles s2, s1 et s0.

Il semble bien que ce style d’encapsulage d’une structure non-mutable est peu utilisé en pratique. En tout cas, la bibliothèque de Java ne propose pas de tels ensembles « fonctionnels ». Les deux avantages de la technique, à savoir une meilleure structuration, et une représentation uniforme des ensembles, y compris l’ensemble vide, comme des objets, ne justifient sans doute pas la cellule de mémoire supplémentaire allouée systématiquement pour chaque ensemble. L’encapsulage se rencontre plus fréquemment quand il s’agit de protéger une structure mutable.

1.4.2  Ensembles mutables

On peut aussi vouloir modifier un ensemble et non pas en construire un nouveau. Il s’agit d’un point de vue impératif, étant donné un ensemble s, appliquer l’opération add(int x) à s, ajoute l’élément x à s. Cette idée s’exprime simplement en Java, en faisant de s un objet (d’une nouvelle classe Set) et de add une méthode de cet objet. On ajoute alors un élément x à s par un appel de méthode s.add(x), et la signature de add la plus naturelle est

La nouvelle signature de add révèle l’intention impérative : s connu est modifié et il n’y a donc pas lieu de le renvoyer après modification.

Pour programmer la nouvelle classe Set des ensembles impératifs, on a recours encore une fois à la technique d’encapsulage. Les objets de la classe Set possèdent une variable d’instance qui est une List. Mais cette fois, les méthodes des objets Set modifient la variable d’instance.

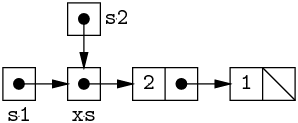
Le champ xs est privé, afin de garantir que la classe Set est la seule à manipuler cette liste. Cette précaution autorise, mais n’impose en aucun cas, l’emploi des listes mutables au prix d’un risque modéré, comme dans la méthode remove qui appelle List.nremove. Le caractère impératif des ensembles Set est clairement affirmé et on ne sera (peut-être) pas surpris par l’affichage du programme suivant :

Le programme affiche {1, 2} car s1 et s2 sont deux noms du même ensemble impératif.

Plus généralement, en utilisant une structure de donnée impérative, on souhaite faire profiter l’ensemble du programme de toutes les modifications réalisées sur cette structure. Cet effet ici recherché est facilement atteint en mutant le champ privé xs des objets Set, c’est la raison même de l’encapsulage.

Solution. On peut écrire d’abord

  void diff(Set s) { this.xs = List.diff(this.xs, s.xs) ; }

Où List.diff est non destructive (voir exercice 1.3), et où on a écrit this.xs au lieu de xs pour bien insister.

Utilsons maintenant les listes mutables. Compte tenu de la sémantique, il semble légitime de modifier les cellules accessibles à partir de this.xs, mais pas celles accessibles à partir de s.xs. On tente donc :

  void diff(Set s) {
    for (List ys = s.xs ; ys != null ; ys = ys.next)
      this.xs = List.nremove(ys.val, this.xs) ;
  }

L’emploi d’une nouvelle variable ys s’impose, car il ne faut certainement pas modifier s.xs. Plus précisément on ne doit pas écrire for ( ; s.xs != null ; s.xs = s.xs.next ). Notons au passage que la déclaration private List xs n’interdit pas la modification de s.xs : le code de diff se trouve dans la classe Set et il a plein accès aux champs privés de tous les objets de la classe Set.

On vérifie que l’auto-appel s.diff(s) est correct, même si c’est de justesse. Supposons par exemple que xs pointe vers la liste (1,(2,(3,∅))). Au début de la première itération, on a

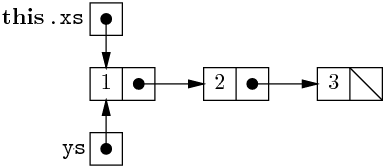
Dans ces conditions, enlever ys.val (1) de la liste this.xs revient simplement à renvoyer this.xs.next. Et à la fin de première itération, on a

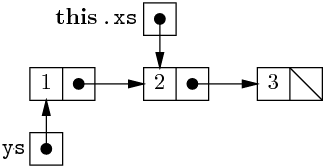
Les itérations suivantes sont similaires : on enlève toujours le première élément de la liste pointée par this.xs, de sorte qu’en début puis fin de seconde itération, on a

Puis au début et à la fin de la dernière itération, on a

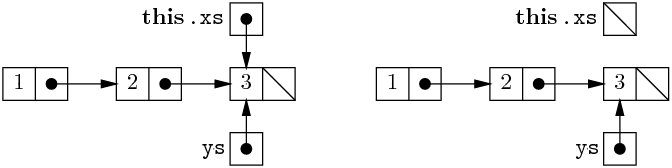
Et donc, this.xs vaut bien null en sortie de méthode diff, ouf. Tout cela est quand même assez acrobatique. □

1.5  Complément : listes bouclées

Des éléments peuvent être organisés en séquence, sans que nécessairement la séquence soit finie. Si la séquence est périodique, elle devient représentable par une liste qui au lieu de finir, repointe sur une de ses propres cellules. Par exemple, on peut être tenté de représenter les décimales de 1/2 = 0.5, 1/11 = 0.090909⋯ et 1/6 = 0.16666⋯ par

Nous distinguons ici, d’abord une liste finie, ensuite une liste circulaire — le retour est sur la première cellule, et enfin une liste bouclée la plus générale.

1.5.1  Représentation des polygones

Plus couramment, il est pratique de représenter un polygone fermé par la liste circulaire de ses sommets. La séquence des points est celle qui correspond à l’organisation des sommets et des arêtes.

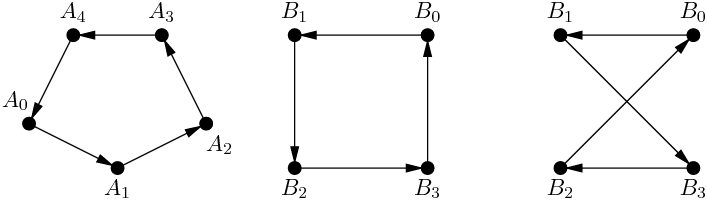
Les polygones étant fermés, les listes circulaires sont naturelles. L’ordre des sommets dans la liste est significatif, ainsi les polygones (B₀B₁B₂B₃) et (B₀B₁B₃B₂) sont distincts.

Pour représenter les polygones en machine, nous définissons une classe des cellules de liste de points.

Tout est privé, compte tenu des manipulations dangereuses auxquelles nous allons nous livrer. La classe Point des points est celle de la bibliothèque (package java.awt), elle est sans surprise : p.x et p.y sont les coordonnées, p.distance(q) renvoie la distance entre les points p et q.

Nous allons concevoir et implémenter un algorithme de calcul de l’enveloppe convexe d’un nuage de points, algorithme qui s’appuie naturellement sur la représentation en machine des polygones (convexes) par les listes circulaires. Mais commençons d’abord par nous familiariser tant avec la liste circulaire, qu’avec les quelques notions de géométrie plane nécessaires. Pour nous simplifier un peu la vie nous allons poser quelques hypothèses.

• Les polygones ont toujours au moins un point. Par conséquent, null n’est pas un polygone.
• Les points sont en position générale. Ce qui veut dire que les points sont deux à deux distincts, et qu’il n’y a jamais trois points alignées.
• Le plan est celui d’une fenêtre graphique Java, c’est à dire que l’origine des coordonnées est en haut et à gauche. Ce qui entraîne que le repère est en sens inverse du repère usuel du plan (l’axe des y pointe vers le bas).

1.5.2  Opérations sur les polygones

L’intérêt de la liste circulaire apparaît pour, par exemple, calculer le périmètre d’un polygone. Pour ce faire, il faut sommer les distances (A₀A₁), (A₁A₂), …(A_n−1A₀). Si nous représentions le polygone par la liste ordinaire de ses points, le cas de la dernière arête (A_n−1A₀) serait particulier. Avec une liste circulaire, il n’en est rien, puisque le champ next de la cellule du point A_n−1 pointe vers la cellule du point A₀. La sommation se fait donc simplement en un parcours des sommets du polygone. Afin de ne pas sommer indéfiniment, il convient d’arrêter le parcours juste après cette « dernière » arête, c’est à dire quand on retrouve la « première » cellule une seconde fois.

L’usage d’une boucle do {…} while (…) (section B.3.4) est naturel. En effet, on veut finir d’itérer quand on voit la première cellule une seconde fois, et non pas une première fois. On observe que le périmètre calculé est 0.0 pour un polygone à un sommet et deux fois la distance (A₀A₁) pour deux sommets.

Nous construisons un polygone à partir de la séquence de ses sommets, extraite d’un fichier ou bien donnée à la souris. La lecture des sommets se fait selon le modèle du Reader (voir section B.6.2.1). Soit donc une classe PointReader des lecteurs de points pour lire les sources de points (fichier ou interface graphique). Ses objets possèdent une méthode read qui consomme et renvoie le point suivant de la source, ou null quand la source est tarie (fin de fichier, double clic). Nous écrivons une méthode de construction du polygone formé par une source de points.

La programmation est récursive pour facilement préserver l’ordre des points de la source. La liste est d’abord lue puis refermée. C’est de loin la technique la plus simple. Conformément à nos conventions, le programme refuse de construire un polygone vide. À la place, il lance l’exception Error avec pour argument un message explicatif. L’effet du lancer d’exception peut se résumer comme un échec du programme, avec affichage du message (voir B.4.2 pour les détails).

Nous nous posons maintenant la question d’identifier les polygones convexes. Soit maintenant P un polygone. La paire des points p.val et p.next.val est une arête (A₀A₁), c’est-à-dire un segment de droite orienté. Un point quelconque Q, peut se trouver à droite ou à gauche du segment (A₀A₁), selon le signe du déterminant det(A₀A₁, A₀P). La méthode suivante permet donc d’identifier la position d’un point relativement à la première arête du polygone P.

Par l’hypothèse de position générale, getSide ne renvoie jamais zéro. Une vérification rapide nous dit que, dans le système de coordonnées des fenêtres graphiques, si getSide(q, p) est négatif, alors le point q est à gauche de la première arête du polygone p.

Un polygone est convexe (et bien orienté) quand tous ses sommets sont à gauche de toutes ses arêtes. La vérification de convexité revient donc à parcourir les arêtes du polygone et, pour chaque arête à vérifier que tous les sommets autres que ceux de l’arête sont bien à gauche.

On note les deux boucles imbriquées, une boucle sur les sommets dans une boucle sur les arêtes. La boucle sur les sommets est une boucle while par souci esthétique de ne pas appeler getSide avec pour arguments des points qui ne seraient pas en position générale.

Pour un polygone à n sommets, la boucle sur les arêtes est exécutée n fois, et à chaque fois, la boucle sur les sommets est exécutée n−2 fois. La vérification de convexité coûte donc de l’ordre de n² opérations élémentaires.

Notons que la méthode getSide nous permet aussi de déterminer si un point est à l’intérieur d’un polygone convexe.

Notons que la convexité permet une définition et une détermination simplifiée de l’intérieur. La méthode isInside a un coût de l’ordre de n opération élémentaires, où n est la taille du polygone.

1.5.3  Calcul incrémental de l’enveloppe convexe

L’enveloppe convexe d’un nuage de points est le plus petit polygone convexe dont l’intérieur contient tous les points du nuage. Pour calculer l’enveloppe convexe, nous allons procéder incrémentalement, c’est-a-dire, en supposant que nous possédons déjà l’enveloppe convexe des points déjà vus, construire l’enveloppe convexe des points déjà vus plus un nouveau point. Soit donc la séquence de points P₀,P₁, … P_k, dont nous connaissons l’enveloppe convexe E = (E₀E₁…E_c), Et soit Q = P_k+1 le nouveau point.

• Si Q est à l’intérieur de E, l’enveloppe convexe ne change pas.
• Sinon, il faut identifier deux sommets E_i et E_j, tels que tous les points de E sont à gauche de (E_iQ) et (QE_j). La nouvelle enveloppe convexe est alors obtenue en remplaçant la séquence (E_i…E_j) par (E_iQE_j).
  
  Sans réaliser une démonstration complète, il semble clair que Q se trouve à droite des arêtes supprimées et à gauche des des arêtes conservées. Mieux, lorsque l’on parcourt les sommets du polygone, le sommet E_i marque une première transition : Q est à gauche de (E_i−1E_i) et à droite de (E_iE_i+1), tandis que le sommet E_j marque la transition inverse. On peut aussi imaginer que Q est une lampe, il faut alors supprimer les arêtes éclairées de l’enveloppe.

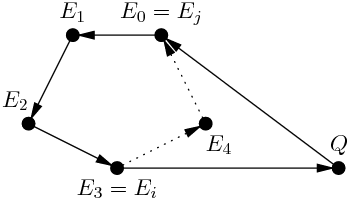
Il faut donc identifier les sommets de E où s’effectuent les transitions « Q à gauche puis à droite » et inversement. Le plus simple paraît de se donner d’abord une méthode getRight qui renvoie la « première » arête qui laisse Q à droite, à partir d’un sommet initial supposé quelconque.

Notons que dans le cas où le point Q est à l’intérieur de E, c’est-à-dire à gauche de toutes ses arêtes, getRight renvoie null. On écrit aussi une méthode getLeft pour détecter la première arête de E qui laisse Q à gauche. Le code est identique, au test getSide(q, p) > 0, à changer en getSide(q, p) < 0, près.

La méthode extend d’extension de l’enveloppe convexe, trouve d’abord une arête qui laisse Q à droite, si une telle arête existe. Puis, le cas échéant, elle continue le parcours, en enchaînant un getLeft puis un getRight afin d’identifier les points E_j puis E_i qui délimitent la partie « éclairée » de l’enveloppe.

La structure de liste circulaire facilite l’écriture des méthodes getRight et getLeft. Elle permet aussi, une fois trouvés E_i et E_j, une modification facile et en temps constant de l’enveloppe convexe. Les deux lignes qui effectuent cette modification sont directement inspirées du dessin d’extension de polygone convexe ci-dessus. Il est clair que chacun des appels à getRight et getLeft effectue au plus un tour du polygone E. La méthode extend effectue donc au pire trois tours du polygone E (en pratique au plus deux tours, en raison de l’alternance des appels à getRight et getLeft). Elle est donc en O(c), où c est le nombre de sommets de l’enveloppe convexe.

Il nous reste pour calculer l’enveloppe convexe d’un nuage de points lus dans un PointReader à initialiser le processus. On peut se convaincre assez facilement que extend fonctionne correctement dès que E possède deux points, car dans ce cas il existe une arête éclairée et une arête sombre. On écrit donc.

Pour un nuage de n points, on exécute de l’ordre de n fois extend, dont le coût est en O(c), sur des enveloppes qui possèdent c ≤ n sommets. Le programme est donc en O(n²). Le temps d’exécution dépend parfois crucialement de l’ordre de présentation des points. Dans le cas où par exemple l’enveloppe convexe est formée par les trois premiers points lus, tous les points suivants étant intérieurs à ce triangle, alors on a un coût linéaire. Malheureusement, si tous les points de l’entrée se retrouvent au final dans l’enveloppe convexe, le coût est bien quadratique. Les sources d’un programme de démonstration sont disponibles sous la forme d’une archive poly.tar.

1. Récupérer l’archive (bouton de droite).
2. La décompacter (tar xf poly.tar).
3. La compiler (cd poly ; javac Poly.java).
4. Exécuter la démo (java Poly). Il faut d’abord saisir deux points à la souris, fermer le polygone (bouton Close), puis entrer les points suivants à la souris.

1.5.4  Calcul efficace de l’enveloppe convexe

L’enveloppe convexe d’un nuage de n points du plan peut se calculer en O(n logn) opérations, à l’aide de l’algorithme classique de la marche de Graham (Graham scan) Nous n’expliquerons pas la marche de Graham, voir par exemple [2, Chapitre 35] ou [7, Chapitre 25]. En effet, un raffinement de la technique incrémentale inspire un algorithme tout aussi efficace, dumoins asymptotiquement. De plus ce nouvel algorithme va nous permettre d’aborder une nouvelle sorte de liste.

Rappelons l’idée de l’algorithme incrémental, sous une forme un peu imagée. L’enveloppe convexe E est soumise à la lumière émise par le nouveau point Q. En raison de sa convexité même, E possède une face éclairée et une face sombre. La face éclairée va du sommet E_i au sommet E_j, et l’extension de l’enveloppe revient à remplacer la face éclairée par E_iQE_j. Supposons connaître un sommet P de l’enveloppe convexe qui est « éclairé » par le nouveau point Q (c’est-a-dire que l’arête issue de P laisse Q à droite). Le sens de rotation selon les next nous permet de trouver la fin de la face éclairée directement, c’est-à-dire sans passer par la face sombre. Pour pouvoir trouver le début de la face éclairée tout aussi directement, il faut pouvoir tourner dans l’autre sens ! Nous allons donc ajouter un nouveau champ prev à nos cellules de polygones, pour les chaîner selon l’autre sens de rotation.

Nos listes de sommets deviennent des listes doublement chaînées (et circulaires qui plus est), une structure de données assez sophistiquée, que nous pouvons illustrer simplement par le schéma suivant :

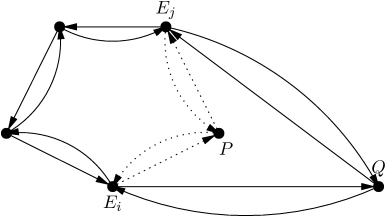
En suivant les champs prev (notés par des flèches courbes), nous trouvons facilement la première arête inverse sombre à partir du point P, c’est-à-dire le premier sommet E_i dont est issue une arête inverse qui laisse le point Q à droite.

Et nous pouvons écrire la nouvelle méthode d’extension de l’enveloppe convexe.

La méthode extend2 identifie la face éclairée pour un coût proportionnel à la taille de cette face. Puis, elle construit la nouvelle enveloppe en remplaçant la face éclairée par (E_iQE_j). Les manipulations des champs next et prev sont directement inspirées par le schéma ci-dessus.

La méthode n’est correcte que si Q éclaire l’arête issue de P. Ce sera le cas, quand

1. P est le point d’abscisse maximale parmi les points déjà vus.
2. Q est d’abscisse strictement supérieure à celle de de P.

En fait l’hypothèse de position générale n’interdit pas que deux points possèdent la même abscisse (mais c’est interdit pour trois points). En pareil cas, pour que Q éclaire l’arête issue de P, il suffit que l’ordonnée de Q soit inférieure à celle de P, en raison de la convention que l’axe des y pointe vers le bas. Autrement dit, P est strictement inférieur à Q selon l’ordre suivant.

On note que le point ajouté Q fait toujours partie de la nouvelle enveloppe convexe. En fait, il sera le nouveau point distingué lors de la prochaine extension, comme exprimé par la méthode complète de calcul de l’enveloppe convexe.

On peut donc assurer la correction de l’algorithme complet en triant les points de l’entrée selon les abscisses croissantes, puis les ordonnées décroissantes en cas d’égalité. Évidemment pour pouvoir trier les points de l’entrée il faut la lire en entier, l’algorithme n’est donc plus incrémental.

Estimons maintenant le coût du nouvel algorithme de calcul de l’enveloppe convexe de n points. On peut trier les n points en O(n logn). Nous prétendons ensuite que le calcul proprement dit de l’enveloppe est en O(n). En effet, le coût d’un appel à extend2 est en O(j−i) où j−i−1 est le nombre de sommets supprimés de l’enveloppe à cette étape. Or un sommet est supprimé au plus une fois, ce qui conduit à une somme des coûts des appels à extend2 en O(n). Le tri domine et l’algorithme complet est donc en O(n logn). Cet exemple illustre que le choix d’une structure de données appropriée (ici la liste doublement chaînée) est parfois crucial pour atteindre la complexité théorique d’un algorithme. Ici, avec une liste chaînée seulement selon les champs next, il n’est pas possible de trouver le sommet E_i à partir d’un sommet de la face éclairée sans faire le tour par la face sombre.

1

En fait, un champ de type objet non-initialisé explicitement contient la valeur par défaut null, voir B.3.3.

2

Attention, ce n’est pas toujours le cas, une allocation de tableau par exemple prend un temps proportionnel à la taille du tableau. Par ailleurs nous négligeons le coût du garbage collector.