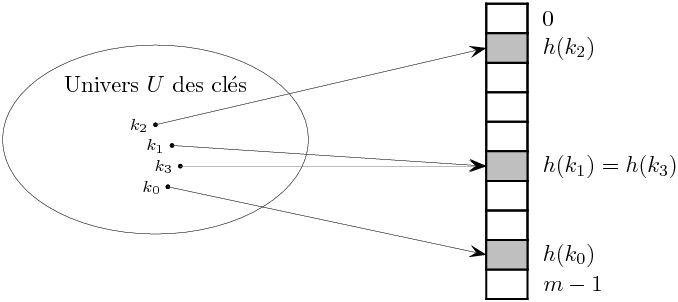
| Figure 3.1: Une collision dans une table de hachage. |



Ce chapitre aborde un problème très fréquemment rencontré en informatique : la recherche d’information dans un ensemble géré de façon dynamique. Nous nous plaçons dans le cadre où une information complète se retrouve normalement à l’aide d’une clé qui l’identifie. La notion se rencontre dans la vie de tous les jours, un exemple typique est l’annuaire téléphonique : connaître le nom et les prénoms d’un individu suffit normalement pour retrouver son numéro de téléphone. En cas d’homonymie absolue (tout de même rare), on arrive toujours à se débrouiller. Dans les sociétés modernes qui refusent le flou (et dans les ordinateurs) la clé doit identifier un individu unique, d’où, par exemple, l’idée du numéro de sécurité sociale,
Nous voulons un ensemble dynamique d’informations, c’est-à-dire aussi pouvoir ajouter ou supprimer un élément d’information. On en vient naturellement à définir un type abstrait de données, appelé table d’association qui offre les opérations suivantes.
La seconde opération mérite d’être détaillée. Lors de l’ajout d’une paire clé-information, nous précisons :
Il en résulte qu’il n’y a jamais dans la table deux informations distinctes associées à la même clé.
Il n’est pas trop difficile d’envisager la possibilité inverse, en ajoutant une nouvelle association à la table dans tous les cas, que la clé s’y trouve déjà ou pas. Il faut alors réviser un peu les deux autres opérations, afin d’identifier l’information concernée parmi les éventuellement multiples qui sont associées à une même clé. En général, on choisit l’information la plus récemment entrée, ce qui revient à un comportement de pile.
Enfin, il peut se faire que la clé fasse partie de l’information, comme c’est généralement le cas dans une base de données. Dans ce cas appelons enregistrement un élément d’information. Un enregistrement est composé de plusieurs champs (nom, prénom, numéro de sécurité sociale, sexe, date de naissance etc.) dont un certain nombre peuvent servir de clé. Il n’y a là aucune difficulté du moins en théorie. Il se peut aussi que l’information se réduise à la clé, dans ce cas la table d’association se réduit à l’ensemble (car il n’y a pas de doublons).
Nous illustrons l’intérêt de la table d’association par un exemple ludique :
un programme Freq qui
compte le nombre d’occurrences des mots d’un texte, dans le but de
produire d’intéressantes statistiques.
Soit un texte, par exemple notre
hymne national, nous aurons
% java Freq marseillaise.txt nous: 10 vous: 8 français: 7 leur: 7 dans: 6 liberté: 6 …
Le problème à résoudre se décompose naturellement en trois :
Supposons les premier et troisième points résolus.
Le troisième par un tri et le premier
par une classe WordReader des flux de mots. Les
objets de cette classe possèdent une méthode read qui renvoie le
mot suivant du texte (un String) ou null à la fin du texte.
Une table d’association permet de résoudre facilement le deuxième point :
il suffit d’associer mots et entiers. Un mot qui n’est pas dans la
table est conventionnellement associé à zéro. À chaque mot lu m on
retrouve l’entier i associé à m, puis on change l’association en
m associé à i+1. Nous pourrions spécifier en français une version
raffinée de table d’association (pas de suppression, information
valant zéro par défaut).
Nous préférons le faire directement en Java
en définissant une
interface Assoc.
La définition d’interface ressemble à une définition de classe, mais
sans le code des méthodes.
Cette absence n’empêche nullement d’employer une interface comme un type,
nous pouvons donc parfaitement écrire une méthode
count, qui compte
les occurrences des mots du texte dans un Assoc t passé en
argument, sans que la classe exacte de t soit connue1.
(Voir B.6.1.3 pour les deux méthodes des String
employées).
Une fois remplie, la table est simplement affichée sur la sortie standard.
Les points de la création du WordReader et du tri de la table
dans sa méthode toString sont supposés résolus,
nous estimerons donc le programme Freq écrit dès que nous aurons
implémenté la table d’association nécessaire.
La technique d’implémentation la plus simple d’une table
d’associations est d’envisager une liste des paires clé-information.
Dans l’exemple de la classe Freq, les clés sont des chaînes et
les informations des entiers, nous définissons donc une classe
simple des cellules de listes.
Nous aurions pu définir d’abord une classe des paires, puis une classe des listes de paires, mais nous préférons la solution plus économe en mémoire qui consiste à ranger les deux composantes de la paire directement dans la cellule de liste.
Nous dotons la classe AList d’une unique méthode (statique,
null étant une liste valide) destinée à retrouver une paire
clé-information à partir de sa clé.
La méthode getCell renvoie la première cellule de la
liste p dont le champ vaut la clé passée en argument.
Si cette cellule n’existe pas, null est renvoyé.
Notons que les chaînes sont comparées par la méthode
equals
et non pas par l’opérateur ==, c’est plus prudent
(voir B.3.1.1).
Cette méthode getCell
suffit pour écrire la classe L des tables d’associations
basée sur une liste d’association
interne.
Les objets L encapsulent une liste
d’association. Les méthodes get et put emploient toutes les
deux la méthode AList.getCell pour retrouver l’information
associée à la clé key passée en argument.
La technique de l’encapsulage est désormais familière, nous l’avons
déjà exploitée pour les ensembles, les piles et les files dans les
chapitres précédents.
Mais
il faut surtout noter une nouveauté : la classe L déclare
implémenter l’interface Assoc (mot-clé implements). Cette
déclaration entraîne deux conséquences importantes.
L possèdent bien les deux méthodes
spécifiées par l’interface Assoc, avec les signatures conformes.
Il y a un détail étrange : les méthodes spécifiées par une interface
sont obligatoirement public.
L peut prendre
le type Assoc, ce qui
arrive par exemple dans l’appel suivant :
L, seulement
l’interface Assoc.
Notre programme Freq fonctionne, mais il n’est pas très
efficace. En effet si la liste d’association est de taille N, une
recherche par getCell peut prendre de l’ordre de N opérations,
en particulier dans le cas fréquent où la clé n’est pas dans la liste.
Il en résulte que le programme Freq est en O(n2) où n est
le nombre de mots de l’entrée.
Pour atteindre une efficacité bien meilleure, nous allons introduire
la nouvelle notion de table de hachage.
La table de hachage est une implémentation efficace de la table d’association. Appelons univers des clés l’ensemble U de toutes les clés possibles. Nous allons d’abord observer qu’il existe un cas particulier simple quand l’univers des clés est un petit intervalle entier, puis ramener le cas général à ce cas simple.
Cette technique très efficace ne peut malheureusement s’appliquer que dans des cas très particuliers. Il faut que l’univers des clés soit de la forme {0, …, n−1}, où n est un entier pas trop grand, et d’autre part que deux éléments distincts aient des clés distinctes (ce que nous avons d’ailleurs déjà supposé). Il suffit alors d’utiliser un tableau de taille n pour représenter la table d’association.
Ce cas s’applique par exemple à la base de donnée des concurrents d’une épreuve sportive qui exclut les ex-æquos. Le rang à l’arrivée d’un concurrent peut servir de clé dans la base de données. Mais, ne nous leurrons pas un cas aussi simple est exceptionnel en pratique. Le fait pertinent est de remarquer que le problème de la recherche d’information se simplifie beaucoup quand les clés sont des entiers pris dans un petit intervalle.
L’idée fondamentale de la table de hachage est de se ramener au cas de l’adressage direct, c’est-à-dire de clés qui sont des indices dans un tableau. Soit m, entier pas trop grand, à vrai dire entier de l’ordre du nombre d’éléments d’informations que l’on compte gérer. On se donne une fonction
| h : U → {0, …, m−1} |
appelée fonction de hachage. L’idée est de ranger l’élément de clé k non pas dans une case de tableau t[k], comme dans l’adressage direct (cela n’a d’ailleurs aucun sens si k n’est pas un entier) , mais dans t[h(k)]. Nous reviendrons en 3.3 sur le choix, relativement délicat, de la fonction de hachage. Mais nous devons affronter dès à présent une difficulté. En effet, il devient déraisonnable d’exclure le cas de clés (distinctes) k et k′ telles que h(k) = h(k′). La figure 3.1 illustre la survenue d’une telle collision entre les clés k1 et k3 distinctes qui sont telles que h(k1) = h(k3).
Figure 3.1: Une collision dans une table de hachage. 
Précisons un peu le problème, supposons que la collision survient lors de l’ajout de l’élément d’information v3 de clé k3, alors qu’il existe déjà dans la table une clé k1 avec h(k1) = h(k3). La question est alors : où ranger l’information associée à la clé k3 ?
La solution la plus simple pour résoudre les collisions consiste à mettre tous les éléments d’information dont les clés ont même valeur de hachage dans une liste. On parle alors de résolution des collisions par chaînage. Dans le cas de l’exemple de collision de la figure 3.1, on obtient la situation de la figure 3.2.
Figure 3.2: Résolution des collisions par chaînage. 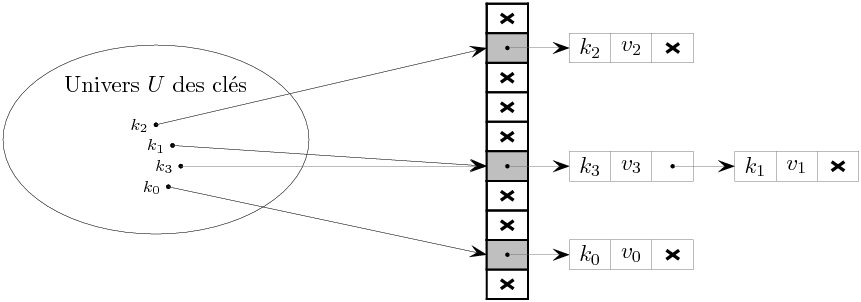
On remarque que les éléments de la table t sont tout bêtement des listes d’association, la liste t[i] regroupant tous les éléments d’information (k,v) de la table qui sont tels que h(k) vaut l’indice i.
Nous proposons une nouvelle implémentation H
des tables d’associations Assoc, en encapsulant cette fois
une table de hachage.
Le code de la fonction de hachage hash est en fait assez
simple, parce qu’il utilise la
méthode de hachage des chaînes
fournie par Java (toute la complexité est cachée dans cette méthode)
dont il réduit le résultat modulo la taille du tableau interne t,
afin de produire un indice valide. La valeur absolue Math.abs
est malheureusement nécessaire, car pour n négatif,
l’opérateur « reste de la division euclidienne » % renvoie un
résultat négatif (misère).
Il est surtout important de remarquer :
L (section 3.1.2), en remplaçant p par t[h].
H déclare implémenter
l’interface Assoc et le fait effectivement ce que le compilateur
vérifie.
Un objet de la nouvelle classe H est donc un argument valide
pour la méthode count de la classe Freq.
Estimons le coût de put et de get pour une table qui contient
N éléments d’information. On suppose que le coût du calcul
de la fonction hachage est en O(1), et que hachage est uniforme,
c’est-à-dire que la valeur de hachage d’une clé vaut h ∈
[0…m[ avec une probabilité 1/m.
Ces deux hypothèses sont réalistes.
Pour la première, en supposant que le coût de calcul
de la fonction de hachage est proportionnel à la longueur des mots,
nous constatons que la longueur des mots
d’un texte ordinaire de N mots est faible et indépendante
de N.2
La seconde hypothèse traduit simplement que nous disposons d’une
« bonne » fonction de hachage, faisons confiance à la méthode
hashCode des String.
Sous ces deux hypothèses, la recherche d’un élément se fait en moyenne en temps Θ(1+α), où α = n/m est le facteur de charge (load factor) de la table (n est le nombre de clés à ranger et m est la taille du tableau). Plus précisément une recherche infructueuse dans la table parcourt en moyenne α cellules de listes, et une recherche fructueuse 1 + α/2 − 1/(2m) cellules, coûts auquels on ajoute le coût du calcul de la fonction de hachage. Ce résultat est démontré dans [2, section 12.2], contentons nous de remarquer que α est tout simplement la longueur moyenne des listes d’associations t[h].
Peut-être faut il remarquer que le coût d’une recherche dans le cas le pire est O(n), quand toutes les clés entrent en collision. Mais employer les tables de hachage suppose de faire confiance au hasard (hachage uniforme) et donc de considérer plus le cas moyen que le cas le pire. Une façon plus concrète de voir les choses est de considérer que, par exemple lors du comptage des mots d’un texte, on insère et recherche de nombreux mots uniformément hachés, et que donc le coût moyen donne une très bonne indication du coût rencontré en pratique.
Dans un premier temps, pour notre implémentation simple de H qui
dimensionne le tableau t initialement, nous pouvons interpréter le
résultat de complexité en moyenne d’une recherche en Θ(1 +
α), en constatant que si la taille du tableau interne est de
l’ordre de n, alors nous avons atteint un coût (en moyenne) de
put et get en temps constant. Il peut sembler que nous nous
sommes livrés à une suite d’approximations et d’à-peu-près, et c’est
un peu vrai. Il n’en reste pas moins, et c’est le principal, que les
tables de hachage sont efficaces en pratique, essentiellement sous
réserve que pour une exécution donnée, les valeurs de hachage des clés
se répartissent uniformément parmi les indices du tableau interne
correctement dimensionné,
mais aussi que le coût du calcul de la fonction de hachage ne soit pas
trop élevé. Dans cet esprit pragmatique, on peut voir la table de
hachage comme un moyen simple de diviser le coût des listes
d’association d’un facteur n, au prix de l’allocation d’un tableau
de taille de l’ordre de n.
Dans un deuxième temps, il est plus convenable, et ce sera aussi plus pratique, de redimensionner dynamiquement la table de hachage afin de maintenir le facteur de charge dans des limites raisonnables. Pour atteindre un coût amorti en temps constant pour put, il suffit de deux conditions (comme pour push dans le cas des piles, voir 2.2.1)
Définissons d’abord une constante alpha qui est notre borne supérieure du facteur de charge, et une variable d’instance nbKeys qui compte le nombre d’associations effectivement présentes dans la table.
Nous avons aussi changé la valeur de la taille par défaut de la table, afin de ne pas mobiliser une quantité conséquente de mémoire a priori. C’est aussi une bonne idée de procéder ainsi afin que le redimensionnement ait effectivement lieu et que le code correspondant soit testé.
La méthode de redimensionnement resize, à ajouter à la
classe H double la taille du tableau interne t.
Il faut noter que la fonction de hachage hash qui transforme les
clés en indices du tableau t dépend de la taille de t (de fait
son code emploie this.t.length). Pour cette raison, le nouveau
tableau est directement rangé dans le champ t de this et une
référence sur l’ancien tableau est conservée dans la variable locale
oldT, le temps de parcourir les paires clé-information contenues
dans les listes de l’ancien tableau pour les ajouter dans le nouveau
tableau t.
Le redimensionnement n’est pas gratuit, il est même assez coûteux,
mais il reste bien proportionnel au nombre d’informations stockées
— sous réserve d’un calcul en temps constant de la
fonction de hachage.
C’est la méthode put qui tient à jour le compte nbKey et
appelle le méthode resize quand le facteur de charge
nbKeys/t.length dépasse alpha.
Notez que le redimensionnement est, le cas échéant, effectué après ajout d’une nouvelle association. En effet, la valeur de hachage h n’est valide que relativement à la longueur de tableau t.
Dans le hachage à adressage ouvert, les éléments d’informations sont stockés directement dans le tableau. Plus précisément, la table de hachage est un tableau de paires clé-information. Le facteur de charge α est donc nécessairement inférieur à un. Étant donnée une clé k on recherche l’information associée à k d’abord dans la case d’indice h(k), puis, si cette case est occupée par une information de clé k′ différente de k, on continue la recherche en suivant une séquence d’indices prédéfinie, jusqu’à trouver une case contenant une information dont la clé vaut k ou une une case libre. Dans le premier cas il existe un élément de clé k dans la table, dans le second il n’en existe pas. La séquence la plus simple consiste à examiner successivement les indices h(k), h(k)+1, h(k)+2 etc. modulo m taille de la table. C’est le sondage linéaire (linear probing).
Pour ajouter une information (k,v), on procède exactement de la même manière, jusqu’à trouver une case libre ou une case contenant la paire (k, v′). Dans les deux cas, on dispose d’une case où ranger (k,v), au besoin en écrasant la valeur v′ anciennement associée à k. Selon cette technique, une fois entrée dans la table, une clé reste à la même place dans le tableau et est accédée selon la même séquence, à condition de ne pas supprimer d’informations, ce que nous supposons.
Pour coder une nouvelle implémentation O de la
table d’association Assoc, qui utilise le hachage avec adressage
ouvert. Nous définissons d’abord une classe des paires clé-information.
Les objets O possèdent en propre un tableau d’objets Pair.
Le code de la classe O est donné par
la figure 3.3.
class O implements Assoc {
private final static int SIZE = 1024 ; // Assez grand ?
private Pair [] t ; // Tableau interne de paires
O() { t = new Pair[SIZE] ; }
private int hash(String key) { return Math.abs(key.hashCode()) % t.length ; }
/* Méthode de recherche de la case associée à key */
private int getSlot(String key) {
int h0 = hash(key) ;
int h = h0 ;
do {
/* Si t[h] est « vide » ou contient la clé key, on a trouvé */
if (t[h] == null || key.equals(t[h].key)) return h ;
/* Sinon, passer à la case suivante */
h++ ;
if (h >= t.length) h = 0 ;
} while (h != h0) ;
throw new Error ("Table pleine") ; // On a fait le tour complet
}
public int get(String key) {
Pair p = t[getSlot(key)] ;
if (p == null) {
return 0 ;
} else {
return p.val ;
}
}
public void put(String key, int val) {
int h = getSlot(key) ;
Pair p = t[h] ;
if (p == null) {
t[h] = new Pair(key, val) ;
} else {
p.val = val ;
}
}
}
Dans le constructeur, les cases du tableau new Pair [SIZE]
sont implicitement initialisées à null (voir B.3.6.2),
qui est justement la valeur qui permet à getSlot d’identifier
les cases « vides ».
La méthode getSlot, chargée de trouver la case où ranger
une association en fonction de la clé,
est appelée par les deux méthodes put et get.
La relative complexité de getSlot justifie cette organisation.
La méthode getSlot peut échouer, quand la table est pleine
— notez l’emploi de la boucle do, voir B.3.4,
ce qui rend la question du dimensionnement du tableau
interne plus critique que dans le cas du chaînage.
O afin de redimensionner
automatiquement le tableau interne, dès que le facteur de charge
dépasse une valeur critique alpha.
null et qu’il faut en
tenir compte.
□On démontre [6, section 6.4] qu’une recherche infructueuse entraîne en moyenne l’examen d’environ 1/2·(1 + 1/(1−α)2) cases et une recherche fructueuse d’environ 1/2·(1 + 1/(1−α)), où α est le facteur de charge et sous réserve de hachage uniforme. Ces résultats ne sont stricto sensu plus valables pour α proche de un, mais les formules donnent toujours un majorant. Bref, pour un facteur de charge de 50 % on examine en moyenne pas plus de trois cases.
Le sondage linéaire provoque des phénomènes de regroupement (en plus des collisions). Considérons par exemple la table ci-dessous, où les cases encore libres sont en blanc :

En supposant que h(k) soit distribué uniformément, la probabilité pour que la case i soit choisie à la prochaine insertion est la suivante
|
Comme on le voit, la case 8 a la plus grande probabilité d’être occupée, ce qui accentuera le le regroupement des cases 4–7. Ce phénomène se révèle rapidement quand des clés successives sont hachées sur des entiers successifs, un cas qui se présente en pratique avec le hachage modulo (voir 3.3), quand les clés sont par exemple les valeurs successives d’un compteur, ou, dans des applications plus techniques, des adresses d’objets qui se suivent dans la mémoire.
Plusieurs solutions ont été proposées pour éviter ce problème. La meilleure solution consiste à utiliser un double hachage. On se donne deux fonctions de hachage h : U → {0, …, m−1} et h′ : U → {1, …, r−1} (r < m). Ensuite le sondage est effectué selon la séquence h(k) + h′(k), h(k) + 2h′(k), h(k) + 3h′(k), etc. Les regroupements ne sont plus à craindre essentiellement parce que l’incrément de la séquence est lui aussi devenu une fonction uniforme de la clé. En particulier en cas de collision selon h, il n’y a aucune raison que les sondages se fassent selon le même incrément. Pour que le sondage puisse parcourir toute la table on prend h′(k) > 0 et h′(k) premier avec m taille de la table. Pour ce faire on peut prendre m égal à une puissance de deux et h′(k) toujours impair, ou m premier et h′(k) strictement inférieur à m (par exemple pour des clé entières h(k) = k modm et h′(k) = 1 + (k mod(m−2))
Dans [6, section 6.4] D. Knuth montre que, sous des hypothèses de distribution uniforme et d’indépendance des deux fonctions de hachage, le nombre moyen de sondages pour un hachage double est environ −ln(1−α)/α en cas de succès et à 1/(1−α) en cas d’échec.3 Le tableau ci-dessous donne quelques valeurs numériques :
| Facteur de charge | 50 % | 80 % | 90 % | 99 % |
| Succès | 1.39 | 2.01 | 2.56 | 4.65 |
| Echec | 2.00 | 5.00 | 10.00 | 100.00 |
Comme on le voit α = 80 % est un excellent compromis. Insistons sur le fait que les valeurs de ce tableau sont indépendantes de n. Par conséquent, avec un facteur charge de 80 %, il suffit en moyenne de deux essais pour retrouver un élément, même avec dix milliards de clés ! Notons que pour le sondage linéaire cet ordre de grandeur est atteint pour des tables à moitié pleines. Tandis que pour le chaînage on peut aller jusqu’à un facteur de charge d’environ 4.
En fixant ces valeurs de facteur de charge pour les trois techniques, nous égalisons plus ou moins les temps de recherche. Examinons alors la mémoire occupée pour n associations. Nous constatons que le chaînage consomme un tableau de taille n/4 plus n cellules de listes à trois champs, soit 3 + n/4 + 5·n cases de mémoire en Java, en tenant compte de deux cases supplémentaires par objet (voir 2.4). Tandis que le sondage linéaire consomme 3 + 2·n + 4·n (tableau et paires), et le double hachage 3 + 5/4·n + 4·n (tableau et paires encore). Le gain des deux dernières techniques est donc minime, mais on peut coder avec moins de mémoire (par exemple en gérant deux tableaux, un pour les clés, un pour les valeurs). L’espace mémoire employé devient alors respectivement 6 + 4·n et 6 + 5/2·n, soit finalement une économie de mémoire conséquente pour le double hachage.
Il aurait été étonnant
que la libraire de Java n’offre pas de table de hachage, tant cette
structure est utile. La classe HashMap est une classe
générique HashMap<K,V>
paramétrée par les classes des clés K et des
informations V (voir 2.2.3).
On écrit donc une dernière implémentation, très courte, de
notre interface Assoc.
La table de hachage t est construite avec la taille initiale
et le facteur de charge par défaut (respectivement 16 et 0.75).
Les méthodes
t.put et
t.get sont celles
des HashMap, qui se comportent comme les nôtres.
À ceci près que clés et informations sont obligatoirement
des objets et que l’appel t.get(key) renvoie null quand la
clé key n’est pas dans la table t, fait que nous exploitons
directement dans notre méthode get. On note la conversion
automatique d’un Integer en int (return val dans le
corps de get) et d’un int en Integer (appel
t.put(key,val) dans put).
Nous nous livrons à une expérience consistant à appliquer le
programme Freq à une série de fichiers contenant du source Java.
Nous mesurons le temps cumulé d’exécution de la méthode count (celle qui
lit les mots un par un et accumule les comptes dans la table
d’association Assoc, section 3.1.1),
pour les quatre implémentations des tables d’associations.
L basée sur les listes d’associations.
H basée sur le hachage avec chaînage (facteur de
charge 4.0, taille initiale 16)
O basée sur le hachage ouvert
(sondage linéaire, facteur de
charge 0.5, taille initiale 16)
Lib basée sur les HashMap de la librairie
(probablement chaînage, facteur de charge 0.75, taille initiale 16)
Toutes les tables de hachage sont redimensionnées automatiquement.
Les résultats (figure 3.4) font clairement apparaître que les listes d’associations sont hors-jeu et que les tables de hachage ont le comportement linéaire attendu et même que toutes les implémentations des tables de hachages se valent, au moins dans le cadre de cet expérience.
En dernière analyse, l’efficacité des tables de hachage repose sur
l’uniformité de la fonction de hachage des chaînes de Java, c’est donc
surtout cette dernière qui se montre performante ici. En voici pour
preuve (figure 3.5) l’histogramme des effectifs des
longueurs des listes de collisions à la fin de l’expérience H
(tableau de taille m = 4096, nombre d’associations n = 16092).
Cette figure montre par exemple qu’il y a un peu plus de 800 listes de
collisions de longueur trois.
En conclusion l’intérêt en pratique des tables de hachage est très important, compte tenu des performances atteintes pour une difficulté de réalisation particulièrement faible (surtout si on utilise la bibliothèque).
Si cela vous intéresse, le source complet de la classe Freq est
donné comme une archive (source count.tar). Attention
quand même, ces programmes dépassent largement le cadre du cours.
Vous pouvez regarder en particulier, la classe
WordReader (source WordReader.java) réalisée avec
un
Scanner (voir B.5.5.2), et le tri final,
par emploi du
tri des List de la classe
Collections effectué dans la classe Sort
(source Sort.java).
L’objet List est fabriqué par la méthode
toString des tables d’associations,
voir par exemple celle
des objets de la classe L (source L.java)
des tables d’association
implémentées par les listes (source AList.java).
Rappelons qu’une fonction de hachage est une fonction h: U → {0, … m−1}. Une bonne fonction de hachage doit se rapprocher le plus possible d’une répartition uniforme. Formellement, cela signifie que si on se donne une probabilité P sur U et que l’on choisit aléatoirement chaque clé k dans U, on ait pour tout j avec 0 ≤ j ≤ m−1,
| P(k) = |
|
En pratique, on connaît rarement la probabilité P et on se limite à des heuristiques. En particulier, on veut souvent que des clés voisines donnent des valeurs de hachages très distinctes.
Le cas que nous traitons ci-dessous est celui où l’univers U est un sous-ensemble des entiers naturels, car on peut toujours se ramener à ce cas. Par exemple, si les clés sont des chaînes de caractères, on peut interpréter chaque caractère comme un chiffre d’une base B et la chaîne comme un entier écrit dans cette base. C’est à dire que la chaîne a0a1…an−1 est l’entier a0·Bn−1 + a1· Bn−2 + ⋯ + an−1. Si les caractères sont quelconques on a B = 216 en Java et B = 28 en C ; si les caractères des clés sont limités à l’alphabet minuscule, on peut prendre B=26 ; etc.
Nous pouvons donc revenir aux fonctions de hachage sur les entiers. Une technique courante consiste à prendre pour h(k) le reste de la division de k par m :
| h(k) = k mod m |
Mais dans ce cas, certaines valeurs de m sont à éviter. Par exemple, si on prend m = 2r, h(k) ne dépendra que des r derniers bits de k. Ce qui veut dire, par exemple, que le début des chaînes longues (vues comme des entiers en base B = 2p) ne compte plus, et conduit à de nombreuses collisions si les clés sont par exemple des adverbes (se terminant toutes par ment). Dans le même contexte, si on prend m = B−1, l’interversion de deux caractères passera inaperçue. En effet, comme (a·B + b) − (b·B + a) = (a−b)(B −1), on a
| a·B + b ≡ b·B + a (mod m ) |
En pratique, une bonne valeur pour m est un nombre premier tel que Bk ± a n’est pas divisible par m, pour des entiers k et a petits.
Une autre technique consiste à prendre
| h(k) = ⌊ m (Ck − ⌊ Ck ⌋) ⌋ |
où C est une constante réelle telle que 0 < C < 1. Cette méthode a l’avantage de pouvoir s’appliquer à toutes les valeurs de m. Il est même conseillé dans ce cas de prendre m = 2r pour faciliter les calculs. Pour le choix de la constante C, Knuth recommande le nombre d’or, C = (√5 − 1)/ 2 ≈ 0,618.
Continuons de considérer les chaînes comme des entiers en
base 216. Ces entiers sont très vite grands, ils ne tiennent plus
dans un int dès que la chaîne est de taille supérieure à 2.
On ne peut donc pas (pour un coût raisonnable, il existe des entiers
en précision arbitraire)
d’abord transformer la chaîne en entier, puis calculer h. Dans le
cas du hachage modulo un nombre premier, il reste possible de calculer
modulo m. Mais en fait ce n’est pas très pratique : la fonction de
hachage (méthode hashCode) des chaînes de Java est indépendante de
la tailles des tableaux internes des tables, puisqu’elle est définie
dans la classe des chaînes et ne prend pas une taille de tableau en
argument. À toute chaîne elle associe un
int qui est ensuite réduit en indice. Selon la
documentation, l’appel
hashCode() de la chaîne a0a1…an−1 renvoie
a0·31n−1 + a1·31n−2 + ⋯ + an−2·31 +
an−1.
Autrement dit le code de hashCode pourrait être celui-ci :
Dans nos tables de hachage nous avons ensuite simplement réduit cet entier modulo la taille du tableau interne.
Le calcul h = 31 * h + this.charAt(k) effectue un mélange
entre une valeur courante de h (qui est la valeur de hachage du
préfixe de la chaîne) et la valeur de hachage d’un caractère de la
chaîne qui est le caractère lui-même, c’est-à-dire son code en
Unicode (voir B.3.2.3).
Le multiplicateur 31 est un nombre premier, et ce n’est pas un
hasard.
L’expérience nous a montré que ce mélange simple fonctionne en
pratique, sur un ensemble de clés qui sont les mots que l’on trouve
dans des sources Java (voir en particulier la figure 3.5).
Pour des clés plus générales cette façon de mélanger est
critiquée [8], mais nous allons nous en tenir à elle.
Car il faut parfois construire nos propres fonction
de hachage, ou plus exactement redéfinir nos propres
méthodes hashCode.
Notre table de hachage H appelle
d’abord la méthode hashCode d’une clé (pour trouver un indice
dans le tableau interne, section 3.2.3),
puis la méthode equals de la même clé
(pour par exemple trouver sa place dans une liste de collision,
section 3.1.2). La table de hachage de la librairie procède
similairement.
Or, même si tous les objets possèdent bien des méthodes hashCode
et equals (comme ils possèdent une méthode toString),
les méthodes par défaut ne conviennent pas.
En effet equals par défaut exprime l’égalité physique
des clés (voir B.3.1.1), tandis que hashCode renvoie
essentiellement l’adresse en mémoire de l’objet !
Il faut redéfinir ces deux méthodes, comme nous avons déjà parfois
redéfini la méthode toString (voir B.2.3).
La classe String ne procède pas autrement,
son hashCode et son equals se basent non pas
sur l’adresse en mémoire de la chaîne, mais sur le contenu des
chaînes.
Supposons donc que nous voulions nous servir de paires d’entiers
comme clés, c’est à dire d’objets d’une classe Pair.
Pour redéfinir hashCode nous utilisons tout simplement le mélangeur multiplicatif.
La méthode redéfinie est déclarée public comme la méthode
d’origine. Il importe en fait de respecter toute la signature de la
méthode d’origine. Or, la signature de la méthode
equals des
Object (celle que nous voulons redéfinir) est :
Nous écrivons donc (dans la classe Pair) :
Pour la conversion de type, voir B.3.2.2.
Évidemment, pour que les tables de hachage fonctionnent correctement il
faut que l’égalité selon equals
(l’appel p1.equals(p2) renvoie true)
entraîne l’égalité des code de hachage
(p1.hashCode() == p2.hashCode()),
ce que la documentation de la bibliothèque appelle le contrat
général de hashCode.


