Gagallium

In 2011, I designed a formally verified C parser for my master's internship. You can refer to our ESOP paper (with François Pottier and Xavier Leroy) to see the details. Here, I am going to explain what problems (and some of their solutions) I have to overcome in order to use it in Compcert, the certified compiler developed at Gallium in Coq.

The parsing engine, an overview

I am not going to go into the details here, but let's get an overview of what was my work of 2011. Here is the big picture:

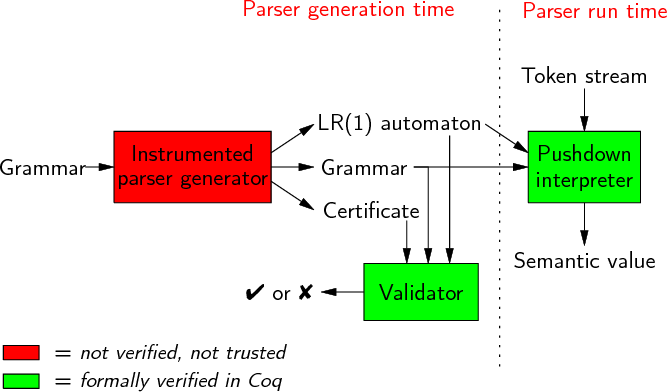
Basically, I added an instrumented Coq backend to the Menhir parser generator. It generates a Coq version of the Grammar, together with an LR(1)-like automaton and a certificate for this automaton. A validator, written in Coq, checks that this certificate is valid, that is that the automaton is related, in some sense, to the grammar.

In order to execute the parser, I developed in Coq an interpreter for LR(1) automatons. It takes a token stream in input and returns a semantic value.

Then, I give a formal proof of the Coq code. Informally, it says that if a given automaton has been validated with respect to a grammar, using some certificate, then I get a correct and complete parser by using the interpreter and the automaton.

What is a correct and complete parser? Correct means that when the parser accepts the input, then returned semantic value is a valid semantic value for the input (which implies that the input word is in the grammar's language). Complete means that if the input word has some semantic value, then the parser will return this semantic value.

One advantage of this approach is that I do not need to prove the generator itself, which is a pretty complicated task. The validation process is not as complicated, as some simple information over the invariants of the automaton is enough. Moreover, one can change the variant of LR(1) automaton (LR(0), LALR, SLR, pager-LR(1), canonical LR(1)...) one wants to use without much work. Note that it does not suffers the typical drawback of translation validation in verified compilation. Typically, the validator performs at run time, and it does not need to validate its input. When it does not, either because it is incomplete or because its input is invalid, the compiler has to fail unexpectedly. Here, as the validation is done at parser generation time, we are sure, once it is generated, that it will perform well.

In order to get more details on this parts, please refer to our ESOP paper.

When theory goes into practice

My final aim when I began this work was to integrate it into Compcert. Besides, before writing the paper, I implemented a proof-of-concept version of Compcert including a verified parser. However, this parser had several more or less critical downsides:

• The context sensitivity of the C grammar makes it impossible to parse it using pure LR(1) technology. This good blog article explains the problem if you are not aware of it. Without entering into the details, our solution worked, but was not fully satisfactory, because the "lexer" was so complicated that it included a full non-certified parser, which could, if buggy, in some corner cases, introduce bugs in the whole parser.
• Parser is a part of a compiler where the performance matters, because it manipulates quite a lot of data. Our approach appears not to be disastrous in terms of performances, but still, in our first implementation, the parser and lexer ran 5 times slower than the previous non-verified Menhir-generated parser.
• It is much more convenient to describe a grammar in the Menhir's description language than directly in Coq. However, the validation of the automaton with respect to a grammar must be done using a Coq form of the grammar. So, actually, one must be confident over the translation of the grammar from Menhir form to Coq form. I tried to make this translation very readable so that someone could check it by hand, but still, it is not very satisfactory

Performance of the extracted code

Internalizing types the right way

After some benchmarking, it appeared that the main bottleneck was the polymorphic hash function of OCaml. Why? Simply because the Coq code needed to manipulate some data that had a type I did not want to formalize in Coq. More details below.

This problem appears typically when you want to manipulate identifiers in Coq: as the naive encoding of strings as lists of characters in Coq is terribly slow, the typical way of using them as identifiers in a Coq code is to build a hash map between some positive numbers and all the identifiers appearing in the source code. The construction of this hash map is done in some OCaml trusted code. Then you can do "efficiently" multiple things on identifiers in the Coq code: you can compare them, you can build maps using them as keys...

However, in my case, I used this technique on the type of location information (that is, the data associated to most of the nodes of the AST to indicate where it comes from). It was very inefficient, because I needed to hash one location information for every very token. Moreover, I do not need to do complex computations on these data. So I figured out that I could use an "abstract type" for these data: I declare it as a Parameter in Coq, and I force extraction to replace it by the right OCaml type. This improved performances a lot.

Using Int31

The other bottleneck was dynamic checks: in order to avoid using too much dependent types in the interpreter (there are already a few of them, and the proofs are complicated enough like that), I put some dynamic checks. I have proved that they will never fail, so there is no problem of correctness here. But still, they exist and they are executed in the extracted code. It was very frustrating because they were consuming quite a lot of time, but I knew they were not useful at all.

These dynamic checks typically verify that the symbols present at the top of the stack correspond to what is expected. This is, from an OCaml point of view, very simple: they consists in comparison of two elements of inductive types of hundreds of constructors without parameters.

However, from a Coq point of view, this is harder: in order to compare values of a type, one needs to provide a decision procedure for equality over this type. Naively, the size of such a decision procedure is (at least) quadratic over the size of the inductive type. Let's take, for example, the case of this simple inductive type:

Inductive T : Type := A:T | B:T

A decision procedure for such a type can be written:

Definition T_eq (x y:T) : bool :=
  match x, y with
  | A, A | B, B => true
  | _, _ => false
  end

However, the kernel of Coq only understands simple pattern matching. So, the frontend desugars it into:

match x with
| A => match y with A => true  | B => false end
| B => match y with A => false | B => true  end
end

This code has quadratic size in the number of constructors. The extraction is smart enough to factorize cases and get some linear length code, but the Coq kernel has to deal with these big terms. Actually, the problem is even worse than it seems: in order to prove that this term is correct directly, it seems necessary to give a term of cubic size...

This is not tractable in our case: the types of data we are comparing typically have a few hundreds of constructors, and the generated term would be enormous, and would take ages to typecheck. A smarter solution is to provide an injection from our type to another Coq type for which I can decide equality easily. Typically, I can provide an injection to the type positive, and that is what I did. This is quite inefficient, because at each comparison, OCaml has to find the corresponding positives, and then compare them bits after bits.

The optimization I used here was to use 31 bits integers provided in the Coq standard library, instead of positives, but it was not as easy as it seemed. Indeed, these integers are internally represented as 31 bits OCaml integers when using the vm_compute tactic, achieving good performance. But they are extracted to OCaml to a bit by bit representation, which have not much better performance than positives. So I had to teach Coq to extract int31 to OCaml's int (which is either 31 bits long or 63 bits long, depending on the architecture). A final care was necessary to make sure that the int31 literals in the Coq source code were really converted to a constant after the whole compilation process (that was not obvious!).

Storing the automaton tables

After these optimization, the performance are about only 2.5 to 3 times slower than the non-certified parser. Based on my benchmarks, one of the bottleneck is the representation of the tables of the automaton: I currently use big match constructs, which does not seem to be as efficient as static arrays, which I do not have in Coq.

However, I don' know a satisfactory solution here (maybe you do?): I think I will let it as is, as the performances are good enough.