Register allocation in CompCert
- August 2, 2012
I am an intern at Gallium this summer. I arrived a week too late to be featured in the Students at Gallium post, so I’ll start by introducing myself. In the fall, I’ll be a fourth year undergraduate at Harvard. Back home, I work with Greg Morrisett as part of the GoNative project. This summer I’m working on optimizations in CompCert. For the past few weeks, I’ve been experimenting with changing the register allocator in CompCert.
Register Allocation in CompCert
At present, CompCert uses a graph-coloring register allocator to
convert from the RTL intermediate
language, which has an unlimited number of pseudo-registers, to the LTL intermediate
language, which uses stack locations and a finite number of machine
registers. Briefly put, the compiler generates a graph where the nodes
are pseudo-registers and machine registers. If there is an edge between
two pseudo-register nodes r1 and r2, this
means that r1 and r2 cannot be assigned to the
same machine register. Similarly, an edge between the pseudo-register
r1 and the machine register mr1 indicates that
r1 cannot be assigned to mr1. Next, we
associate a color with each machine register. Then, the compiler
attempts to color the graph using this palette of colors. That is, it
tries to find a way to assign colors to each node in the graph such that
no adjacent nodes have the same color. Any such coloring corresponds to
a valid assignment of pseudo-registers to machine registers. However,
it’s not always possible to find such a coloring. In this case, the
compiler needs to spill some pseudo-registers. These pseudo-registers
are stored on the stack instead of being assigned to machine
registers.
This is a very elegant way to formulate the problem of register allocation. However, finding a valid coloring of a graph is NP-complete! This might seem alarming at first, but the problem of register allocation is itself NP-complete (via a reduction from the other direction), so we’re no worse off. Anyway, this means we need to resort to heuristics to find a coloring. Specifically, CompCert uses Iterated Register Coalescing (IRC) [George and Appel 1996]. This algorithm is very effective, but it’s also quite complicated. In CompCert, this algorithm is not proven correct. Instead, after generating the graph, the compiler calls an OCaml implementation of IRC and then checks that the coloring is valid. If the checker confirms that the coloring is valid, the compiler uses it and proceeds along. If it does not confirm that it’s valid, compilation is aborted. This checker is proven correct, and because it is simpler, its proof of correctness is easier. One other benefit of this design is that one could swap in a different coloring algorithm without having to reprove anything. The flip side is that the compilation process may simply abort if the OCaml code does not find a coloring that satisfies the checker. Although no wrong code will be generated in this case, it might still be frustrating if the compiler fails to compile something.
A few years ago, Blazy, Robillard, and Appel formally verified the correctness of an implementation of IRC in Coq and used it in CompCert [Blazy et al. 2010]. This approach avoids the downside I just described, but it also required an impressive effort: the proof is 4,800 lines long. Around the same time, Rideau and Leroy implemented a translation validator for register allocation [Rideau and Leroy 2010]. Instead of just validating that the graph is colored correctly, here the entire translation from RTL to LTL can be performed by some unproven piece of code, and then a validator checks that the translation was correct. This allows an even more flexible approach, whereby a variety of different algorithms can be used for register allocation without needing to do new proofs. Previously, Tristan and Leroy explored the use of translation validation for a variety of optimizations [Tristan and Leroy 2008; Tristan and Leroy 2009; Tristan and Leroy 2010]. At present, neither the implementation of IRC in Coq nor the translation validator from RTL to LTL are used in the official release of CompCert.
An Example
So, why bother changing the register allocator? As I mentioned above, the LTL intermediate language uses machine registers and stack locations as operands in its instructions. In reality, not all architectures let you use memory locations as operands in all istructions. Even on CISC architectures like x86, often only one operand may be a location in memory. CompCert’s intermediate language Linear reflects this constraint. Therefore, when translating down to Linear, the compiler inserts instructions to load stack slot operands into temporary registers, uses these temporary registers in the computation, and then stores the contents of these temporary registers back on the stack (if necessary).
Because the inserted loads and stores happen right before and after the instruction where the stack slot operand is used, this can potentially lead to inefficiencies. Consider the following piece of C code:
int evil(int x1, int x2, int x3, int x4, int x5, int x6, int x7, int x8) {
int i;
int y = 0;
int times = x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8;
for(i = 0; i < times; i++) x1 += x1;
for(i = 0; i < times; i++) x2 += x2;
for(i = 0; i < times; i++) x3 += x3;
for(i = 0; i < times; i++) x4 += x4;
for(i = 0; i < times; i++) x5 += x5;
for(i = 0; i < times; i++) x6 += x6;
for(i = 0; i < times; i++) x7 += x7;
for(i = 0; i < times; i++) x8 += x8;
return x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8;
}Now let’s examine the RTL that CompCert 1.10 generates from this C code.
f(x8, x7, x6, x5, x4, x3, x2, x1) {
64: x10 = 0
63: x24 = x8 + x7 + 0
62: x23 = x24 + x6 + 0
61: x22 = x23 + x5 + 0
60: x21 = x22 + x4 + 0
59: x20 = x21 + x3 + 0
58: x19 = x20 + x2 + 0
57: x9 = x19 + x1 + 0
56: x11 = 0
55: nop
54: if (x11 <s x9) goto 53 else goto 50
53: x8 = x8 + x8 + 0
52: x11 = x11 + 1
51: goto 54
50: x11 = 0
49: nop
...
14: x11 = 0
13: nop
12: if (x11 <s x9) goto 11 else goto 8
11: x1 = x1 + x1 + 0
10: x11 = x11 + 1
9: goto 12
8: x18 = x8 + x7 + 0
7: x17 = x18 + x6 + 0
6: x16 = x17 + x5 + 0
5: x15 = x16 + x4 + 0
4: x14 = x15 + x3 + 0
3: x13 = x14 + x2 + 0
2: x12 = x13 + x1 + 0
1: return x12
}We see here that the pseudo-register x9 stores the value
of the times variable. Lines 56-51 and 14-9 correspond to
the first and last of the for loops in the original C program. Now, what
happens when CompCert translates this into LTL? On x86-32, because of
the limited number of registers it will need to spill some of the
pseudo-registers. Examining the LTL output, we see:
f(local(int,3), SI, local(int,0), local(int,1), local(int,4), DI, local(int,2), BP) {
AX = local(int,3) + SI + 0
AX = AX + local(int,0) + 0
AX = AX + local(int,1) + 0
AX = AX + local(int,4) + 0
AX = AX + DI + 0
AX = AX + local(int,2) + 0
BX = AX + BP + 0
AX = 0
54:
if (AX >=s BX) goto 50
local(int,3) = local(int,3) + local(int,3) + 0
AX = AX + 1
goto 54
50:
AX = 0
...
14:
AX = 0
12:
if (AX >=s BX) goto 8
BP = BP + BP + 0
AX = AX + 1
goto 12
8:
AX = local(int,3) + SI + 0
AX = AX + local(int,0) + 0
AX = AX + local(int,1) + 0
AX = AX + local(int,4) + 0
AX = AX + DI + 0
AX = AX + local(int,2) + 0
AX = AX + BP + 0
return AX
}Pseudo-registers x9 and x1 have been
assigned to registers BX and BP respectively.
However, pseudo-register x8 has been stored in stack slot
local(int,3). We can’t examine the Linear intermediate
language output, which is where the spills and reloads are inserted, but
we can examine the Mach output,
which is the subsequent phase. Let’s just focus on the first for loop,
since this phase is more verbose:
AX = 0
54:
if (AX >=s BX) goto 50
DX = stack(16, int)
CX = DX
DX = DX + CX + 0
stack(16, int) = DX
AX = AX + 1
goto 54
50:
AX = 0What happens is that for every iteration of the loop, the value of
stack slot 16 is loaded into DX. This is then doubled, and
the result is stored back into stack slot 16. However, this is somewhat
silly, we could instead move stack(16, int) into
DX once before the loop starts, and then store
DX back into stack(16, int) after the loop is
over like so:
DX = stack(16, int)
AX = 0
54:
if (AX >=s BX) goto 50
CX = DX
DX = DX + CX + 0
AX = AX + 1
goto 54
50:
stack(16, int) = DX
AX = 0This would eliminate many memory accesses. In fact, this is what gcc
and clang do when compiling on -O1. With x1 through
x8 set to 10,000,000, this takes 1.3 seconds when compiled
with CompCert 1.10. In contrast, using gcc -01, it only takes .269s.
Now, naturally there are many other optimizations that gcc is performing
here, so not all of this can be attributed to the register allocation.
Also, this is not at all a realistic benchmark, but it does illustrate a
potential source of improvement.
Alternatives
A common technique that solves the above problem is live-range splitting [Cooper and Simpson 1998]. For some reason, instead of implementing this standard, well accepted solution (which would have made a lot of sense), I decided to try using something crazy and more experimental.
As I mentioned earlier, finding an optimal register allocation is NP-complete. A number of papers have tried to solve register allocation by formulating it as an integer linear program and then throwing an integer linear program solver at it [Goodwin and Wilken 1996].
I decided to try this approach as well. At first I used the formulation in SARA [Nandivada and Palsberg 2006], but I had trouble getting the constraints to work. I switched over to an approach by Appel and George which splits the register allocation problem into two parts [Appel and George 2001]. In the first phase, an integer linear program is formulated to find where to spill and reload pseudo-registers, with the goal of minimizing the number of spills and reloads. In other words, this just decides which pseudo-registers should be stored in the stack and which should be in machine registers at each point, but not which machine registers they should use. The constraints ensure that at each point, the number of pseudo-registers that are supposed to be mapped to machine registers is no more than the number of machine registers available.
In the next phase, these loads and stores are inserted, and then the problem of deciding which pseudos are put in which machine registers is solved by graph coloring.
However, even though the loads and stores have been inserted so as to guarantee that the number of live pseudo-registers is less than or equal to the number of machine registers, this doesn’t mean the graph is colorable! Consider the following example, which is based off of one in the paper. Suppose there are only two machine registers and our program looks like this:
1: y = x + 1;
2: if(x > y) return 0
3: z = 2;
4: if(z > y) return 1
5: x = z + 3
6: return x > zIgnore the fact that some of this is dead code that could be
eliminated. Note that at each point, at most two registers are live at a
time (assuming I haven’t made a mistake…). However, x
interferes with y and z, y
interferes with x and z, and z
interferes with x and y. The resulting
interference graph is a triangle, and it is impossible to color it with
only two colors.
To get around this, at each point in the program, Appel and George create a new fresh pseudo-register for each live pseudo-register and use a parallel move to copy the contents of the old pseudo-registers into these new fresh pseudo-registers. This is enough to guarantee that the degree of each node in the interference graph is less than the number of colors available, which ensures that the graph is colorable.
The problem is now of course that we’ve added in all of these extra
moves. One detail I omitted in my description of IRC above is the idea
of coalescing. If there is a move between pseudo x1 and
x2, and x1 and x2 don’t
interfere, the coloring algorithm tries to assign them the same color.
If it successfully does this, say by assigning them to register
AX, then the move instruction x1 = x2 turns
into AX = AX, and it may be eliminated. The algorithm
coalesces two nodes in the graph in this manner when it can be certain
that by doing so it will not render the graph uncolorable. So, in the
Appel and George approach, the key in the second phase is to get a high
degree of coalescing so that many of these extra moves can be
removed.
Implementing the algorithm
In order to implement this I had to first change the syntax and semantics of the LTL language so that it was closer to the Linear language: operands would have to be machine registers, instructions to load and store stack slots were added, and parameters for functions would be stored according to calling conventions. Next I fixed up the translation from LTL to Linear (in Compcert 1.10 and 1.11 there is another intermediate language called LTLin in between these two, which I removed) and the corresponding proofs.
I decided to re-use the translation validator of Rideau and Leroy. In order to do so, I had to update it because a number of details have changed in CompCert since that work was done: instructions for jumptables and builtin functions have been added to RTL and LTL, the memory model has changed, and the semantics of temporary machine registers are different in LTL. In addition, I had just made my own changes to LTL, so I needed to add support for that as well.
Finally, I had to implement the unproven algorithm in Ocaml and remove plenty of bugs in it (which would have triggered alarms by the validator). I reused the IRC implementation in CompCert for the second phase. In order to fix bugs, I used the Creduce tool [Regehr et al. 2012], and it worked very well for reducing the programs in CompCert’s test and benchmark suite that I was miscompiling.
Results
After all that work, let’s look at the results. Compiling the motivating example from before we get (with x1 through x8 = 10,000,000):
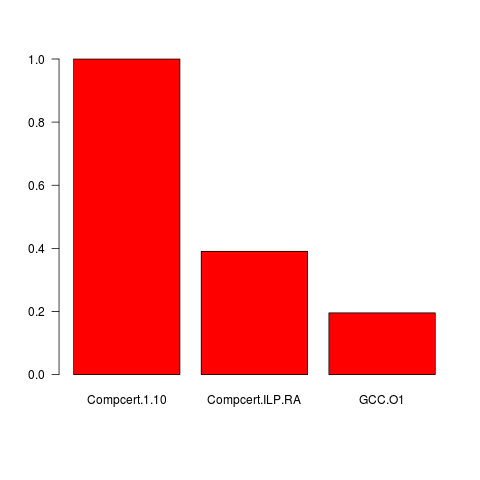
Note that in the above graph, the runtimes are normalized so that CompCert 1.10 has a value of 1. So, the new register allocator is not enough to give performance as good as gcc -O1, but still a vast speedup. Of course, as I said earlier, this is an unrealistic example. How does it fare with the standard benchmarks that are distributed with CompCert?
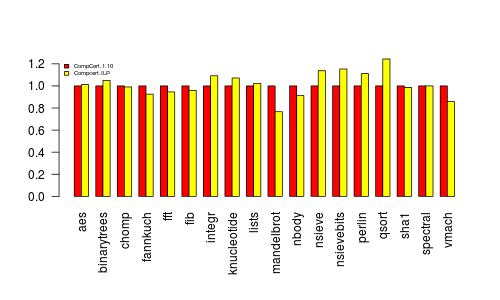
Well, not so impressive. First, note that some benchmarks are excluded here because GLPK ran out of memory while trying to solve the associated integer linear program. Second, it took about 5 minutes (of clock time) to compile all of these programs, whereas CompCert 1.10 takes 2 seconds on the same machine. So, why aren’t the results so great?
Not enough coalescing: Appel and George argue that IRC is just too conservative in its coalescing to eliminate enough of the extra moves that are inserted. They propose using optimistic coalescing [Park and Moon 2004] and even held a contest for better coalescing algorithms. Grund and Hack proposed a method to optimally solve the coalescing problem via integer linear programming with more reasonable runtimes than a naive formulation [Grund and Hack 2007]. I implemented optimal coalescing with ILP, but without the techniques proposed by Grund and Hack, so it was quite slow. It reduced the gap on the qsort benchmark, but CompCert 1.10 still performed better.
Edge splitting: We need to insert the parallel move code to copy contents of pseudo-registers before every instruction. But what happens when there is a merge point in the control flow graph? We need to copy over different pseudos for each of the predecessors of the merge point. Normally we can just put the copy directly after the predecessor itself - but what if the predecessor is itself a branch? Then we need to insert a new basic block that does the parallel move, and then jump back to where we are supposed to go. This is called edge splitting. If we’re not clever with where we place this new block, the extra jumps and indirection could slow things down. I experimented with a bunch of different heuristics for CompCert to use when it linearizes this code, and sometimes the performance on various benchmarks could swing dramatically.
Stack frame sizes: CompCert 1.10’s register allocator tries to assign non-interfering spilled pseudo-registers to use the same stack slots in order to cut down on the number of stack slots needed. At present, my implementation uses one stack slot for each pseudo-register in the original RTL function. In theory this could lead to worse cache performance if the stack frame is huge. To see if this was a factor I made CompCert use much larger stack frames than usual, but this had little impact.
Cost objective: The ILP tries to minimize the “cost” of the spills and reloads it uses. Of course, one has to choose some way to assign costs to the insertion of spills and reloads. I used a simple model where each spill and reload cost 1 unit if it was outside of a loop, and 10 units if it was located inside of a loop. A more precise estimate of execution frequencies (or the use of profile information) might yield better results. Of course, this same data could also be used to improve the current register allocator for CompCert as well.
There could be some other factors I am missing. So to summarize: so far my implementation of this allocator does better on some pathological extreme cases, but results on real benchmarks are more mixed. Moreover, register allocation is another problem where translation validation can effectively reduce proof burden and allow for experimentation with different heuristics.
References:
Appel, A.W. and George, L., 2001. Optimal spilling for CISC machines with few registers. In Proceedings of the ACM SIGPLAN 2001 conference on Programming language design and implementation. New York, NY, USA: ACM, pp. 243–253.
Blazy, S., Robillard, B. and Appel, A.W., 2010. Formal verification of coalescing graph-coloring register allocation. In Proceedings of the 19th European conference on Programming Languages and Systems. Berlin, Heidelberg: Springer-Verlag, pp. 145–164.
Cooper, K.D. and Simpson, L.T., 1998. Live Range Splitting in a Graph Coloring Register Allocator. In Proceedings of the 7th International Conference on Compiler Construction. London, UK, UK: Springer-Verlag, pp. 174–187.
George, L. and Appel, A.W., 1996. Iterated register coalescing. ACM Trans. Program. Lang. Syst., 18, pp.300–324.
Goodwin, D.W. and Wilken, K.D., 1996. Optimal and Near-optimal Global Register Allocation Using 0–1 Integer Programming. Software: Practice and Experience, 26, pp.929–965.
Grund, D. and Hack, S., 2007. A fast cutting-plane algorithm for optimal coalescing. In Proceedings of the 16th international conference on Compiler construction. Berlin, Heidelberg: Springer-Verlag, pp. 111–125.
Nandivada, V.K. and Palsberg, J., 2006. SARA: combining stack allocation and register allocation. In Proceedings of the 15th international conference on Compiler Construction. Berlin, Heidelberg: Springer-Verlag, pp. 232–246.
Park, J. and Moon, S.-M., 2004. Optimistic register coalescing. ACM Trans. Program. Lang. Syst., 26, pp.735–765.
Regehr, J., Chen, Y., Cuoq, P., Eide, E., Ellison, C. and Yang, X., 2012. Test-case reduction for C compiler bugs. In Proceedings of the 33rd ACM SIGPLAN conference on Programming Language Design and Implementation. New York, NY, USA: ACM, pp. 335–346.
Rideau, S. and Leroy, X., 2010. Validating register allocation and spilling. In Compiler Construction (CC 2010). Springer, pp. 224–243.
Tristan, J.-B. and Leroy, X., 2010. A simple, verified validator for software pipelining. In 37th symposium Principles of Programming Languages. ACM Press, pp. 83–92.
Tristan, J.-B. and Leroy, X., 2008. Formal verification of translation validators: A case study on instruction scheduling optimizations. In 35th symposium Principles of Programming Languages. ACM Press, pp. 17–27.
Tristan, J.-B. and Leroy, X., 2009. Verified Validation of Lazy Code Motion. In Programming Language Design and Implementation 2009. ACM Press, pp. 316–326.