Contexte informatique
Un programme à trous quad.ml est fourni.
Il suffit de le récupérer et de le modifier.
Le programme a recours à la librairie Graphics.
Pour le compiler, il faut spécifier explicitement la libraire, à savoir :
% ocamlc -o quad graphics.cma quad.ml
Et on produira l'exécutable quad. Cet exécutable dessine
des images, puis s'arrête.
L'affichage des images est contrôlé à
l'aide des touches du clavier, à tout moment la touche « q » (avec le
curseur de la souris dans la fenêtre graphique) permet de
passer à la question suivante.
Les quadtrees
On présente ici une méthode originale de représentation d'images sous forme d'arbres. Cette représentation donne une méthode de compression plus ou
moins efficace et facilite certaines opérations sur les images.
Pour simplifier, on suppose les images carrées, de côté 2n, et en
noir et blanc.
L'idée est la suivante :
une image toute blanche ou toute noire se représente par sa couleur, tandis
qu'une image composite se divise naturellement en quatre
images carrées.
Selon ce schéma, les images sont représentées par des arbres du type
suivant :
type couleur = Blanc | Noir
type arbre = Feuille of couleur | Noeud of arbre * arbre * arbre * arbre
Les images bitmap étant quand à elles représentées par des
matrices de couleurs que l'on supposera toujours de côté 2n par la
suite.
type image = couleur array array (* matrice de taille 2n *)
1 Echauffement
Écrire une fonction compte_feuilles qui prend un arbre en
argument et renvoie le nombre de feuilles de cet arbre.
Une fonction compte_feuilles grossièrement fausse est présente
dans le squelette quad.ml, à vous de la
remplacer par la bonne.
2 Diverses conversions
Arbre d'une image bitmap
Écrire une fonction image_vers_arbre qui prend un entier k et
une image de côté k, et qui
qui rend l'arbre représentant cette image.
En Caml, étant donné une matrice m, on accède à mji par
m.(i).(j) (car en Caml, une matrice est en fait un tableau de
tableaux, ces derniers étant ici conventionnellement les lignes).
Vous aurez peut-être besoin de consulter la documentation du module
Array.
Dessin de l'image
Nous pourrions inverser la fonction précédente.
Mais il revient quasiment au même de dessiner l'image encodée par un
arbre dans la fenêtre graphique.
Donc écrire une fonction dessine_arbre qui prend un entier k = 2n en argument et
un arbre a, et qui dessine l'image encodée par a dans la
fenêtre graphique opportunément taillée en k × k.
Vous aurez certainement besoin de la fonction
Graphics.fill_rect qui colorie un rectangle dans la
couleur courante (ici le noir).
Les fonctions de test de quad.ml se chargent de la mise en
place de la fenêtre et des appels à image_vers_arbre et à
dessine_arbre.
Normalement, vous deviez obtenir ce dessin :
(Si vous obtenez une isométrie quelconque de ce dessin, tranquilisez
vous et continuez...).
3 Transformations de l'arbre
Écrire les fonctions inverse, rotate et
antirotate qui prennent toutes un arbre a représentant une
image i en argument et
renvoient un arbre représentant l'image inversée de i (blanc et noir
échangés), i tournée d'un quart de tour vers la gauche, et i tournée
d'un quart de tour vers la droite.
Le squelette permet de tester ces trois fonctions. Ainsi,
la séquence de touches «n, i, p » devrait normalement donner ces
images successivement :
4 Une fractale
Écrire une fonction fractale : int -> arbre qui prend un
entier n en argument et construit l'arbre correspondant à n
itérations du processus dont on montre ici les trois premières
applications.
(Il convient ici de bien regarder la première itération pour trouver le
processus.)
5 Sauvegarde des images compressées
Dans le but de sauvegarder les images dans des fichiers,
on se pose le problème de transformer le type arbre en une liste de 0 et
de 1, ainsi que le problème réciproque.
On note code(a) la liste de 0 et de 1 représentant un arbre a. On
choisit le codage suivant :
| code(Feuille Blanc) |
= |
00 |
| code(Feuille Noir) |
= |
01 |
| code(Noeud (a1,a2,a3,a4)) |
= |
1 code(a1) code(a2) code(a3) code(a4) |
Pour simplifier on va procéder en deux temps, d'abord codage (et
décodage) de
l'arbre en liste de bits, puis écriture (et lecture) des bits dans un fichier.
Des arbres vers les listes, et retour
On se donne d'abord un type des bits (zéro ou un).
type bit = Zero | Un
Écrire une fonction arbre_vers_liste de type
arbre -> bit list qui transforme un arbre en une liste de 0 et
de 1 selon le codage. Cette fonction ressemble furieusement à
l'affichage d'un arbre sous forme préfixe.
Écrire la fonction réciproque liste_vers_arbre
de type bit list -> arbre, qui
transforme une liste de bits en l'arbre correspondant.
Cette fonction ressemble furieusement à l'anayse syntaxique d'une
expresssion donnée sous forme préfixe, le codage choisi évitant les
ambiguïtés.
Écriture et lecture
Terminer la question c'est à dire écrire les fonctions
ecrire_arbre de type string -> arbre -> unit
et lire_arbre de type string -> arbre, qui
respectivement sauvegarde un arbre dans un fichier dont le nom est
passé en argument, et lit l'arbre contenu dans un fichier.
On cherche bien évidemment à produire les fichiers les plus petits
possible. L'idée est simple et classique, les fichiers étant des
suites de caractères qui sont aussi des entiers sur 8 bits. On va
donc grouper les bits par paquets de 8 dans des entiers normaux,
convertir ces entiers en caractères (voir Char.chr), puis
écrire les caractères dans le fichier.
Les fonctions sur les fichiers sont regroupées dans le
module Pervasives (ouvert par défaut, ainsi on est pas obligé
de faire précéder ces fonctions de Pervasive.).
On portera un intérêt tout particulier à l'ouverture
(open_out et open_in) et à la fermeture
(close_out et close_in)
d'un fichier, ainsi qu'à l'écriture et à la lecture d'un caractère
(output_char et input_char).
Le squelette fourni contient un test (sauver et relire une des
fractales de la questions précédente), mais vous pouvez aussi lire
cette image.
Programme-solution
This document was translated from LATEX by
HEVEA.
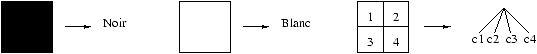
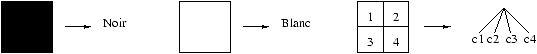

 – n –>
– n –>  – i –>
– i –>  – p –>
– p –> 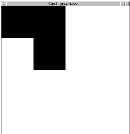
 – n –>
– n –>  – n –>
– n –>  – n –>
– n –>