Types et modularité.
Postscript, PDF Didier Rémy Polytechnique, INRIA
Cours (super, frames) [man]
[doc] [type-index] Exercices
  1. La programmation par les types
  2. Repliages et itérateurs
  3. Separation des concepts
  1. Fold (*)
  2. Fold structuré (*)
  3. Ramassage efficace (*)
  4. Unification (*)



La programmation dirigée par les données

Une idée forte en programmation est que la programmation est dirigée par les données. Cela signifie que la représentation des données induit naturellement des algorithmes de manipulation des données.

En quelque sorte, le choix de représentation des données joue un rôle primordiale dans cette vision. Ne vous a-t-on jamais dit:
    ·Les listes sont des structures de données récursives, donc elles se parcourent naturellement par des fonctions récursives?
    ·Inversement, les tableaux qui sont une structure de donnée énumérée se parcourent plus par des boucles for.
Commes toutes règles, elles sont sujettent à exceptions, bien sûr.

Une librairie qui implémente une structure de donnée complexe est en général accompagnée de fonctions permettant la manipulation ``naturelle'' de cette structure.

La programmation par les types

La programmation polytypique prolonge l'idée de programmation dirigée par les données. Comme les types sont la représentation des données, la programmation est donc au final dirigée par les types.

Une collection peut être représentée par une liste, un tableau ou un ensemble, mais les opérations élémentaires sur les collections restent indépendentes de la représentation:

    ·(find) Trouver un élément
    ·(iter) Itérer une opération (effet de bord) sur chaque élément
    ·(map) Éventuellement, transformer une collection en une autre de même structure (map)
    ·(fold) Appliquer une transformation sur les éléments de la collection en collectant les résultats. Ici la collection des résultats est une fonction passée en paramètre, donc pas nécessairement dans la même structure.
Les librairies List, Array, Set, Map, etc. fournissent toutes ces opérations de bases, mais chaque fois implémentés manuellement.

Programmation polytypique

Dans une certaine mesure, certains opérations pourraient être déduites de la structure de type.

Prenons par exemple, une définition des arbres binaires.
type ('a) tree = Leave of 'a | Node of 'a tree * 'a tree;;
Il y a un itérateur ``naturel'' sur cette structure:
let rec iter_tree f = function
  | Leave x -> f x
  | Node (a, b) -> iter_tree f a; iter_tree f b;;
ainsi qu'un homomorphisme ``naturel'':
let rec map_tree f = function
  | Leave x -> Leave (f x)
  | Node (a, b) -> Node (map_tree f a, map_tree f b);;
La fonction fold, graphiquement

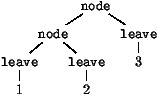
La forme de repliage d'une structure de donnée, qui généralize iter ou map n'est guère plus difficile:

    tree_fold leavenode

Retourne l'arbre de calcul:
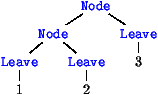
Noter le parallèle entre données et calcul
Fold (le code)

let rec tree_fold leave node =
  let rec fold = function
    | Leave x ->
        leave x
    | Node (t1, t2) ->
        node (fold t1) (fold  t2)
  in fold;;
La traduction peut se laisser guider par les types comme suit: la fonction tree_fold prend autant d'arguments a1 ... an que le type tree a de constructeurs A1 ... An.

Chaque fonction ai est d'aritée égale à celle du constructeur Ai et l'application tree_fold a1 ... anv revient à remplacer dans v chaque constructeur Ak par la fonction ak, puis à évaluer l'expression résultante.

Fold (example)

Appliquer tree_fold leavenode à
Node (Node (Leave 1, Leave 2), Leave3)
revient à évaluer
node (node (leave 1) (leave 2)) (leave3).
Ce que l'on peut vérifier sur un cas concret:
     tree_fold succ ( * )
     (Node (Node (Leave 1, Leave 2), Leave 3))
                     =
     let leave = succ in let node = ( * ) in
     node (node (leave 1) (leave 2)) (leave 3);;
- : bool = true

Cas particuliers

En utilisant la définition précédente, la fonction list_fold est égale à fold_right (modulo réarrangement des arguments):
let list_fold cons nil list =
  List.fold_right cons list nil;;
Cette fonction n'est pas récursive-terminale. Pour le cas particulier des listes, on utilise couramment fold_left qui est récursive terminale. Cela revient à appliquer fold_right sur la liste retournée.

  fold_left cons' nilt produit le même résultat que   list_fold cons nil (reverse t) où cons' xy is cons yx.

(Bien sûr le calcul est effectué directement sans retournement de la liste.)

La forme fold_left est une particularité des listes et ne se généralise pas: dès qu'il y a plusieurs directions de récursion, il n'y a plus de forme récursive terminale évidente.

Size

C'est un cas particulier de tree_fold: chaque fonction ak retourne un entier qui mesure la taille du sous-arbre issu de Ak correspondant, qui ne doit dépendre que la taille que de Ak et de la taille des sous-arbres respectifs.

Version spécialisée de fold
let tree_size leave node t : int = tree_fold leave node t;;
val tree_size : ('a -> int) -> (int -> int -> int) -> 'a tree -> int


Pour les listes

La fonction length est une instance de size qui prend zéro pour le poids de du noeud [] et 1 pour le poid du noeud ::.
let length a_list =
  list_fold (fun a length -> length + 1) 0 a_list;;
Iterators

C'est un cas particulier de fold: chaque function ak retourne ().

Dans les itérateurs, les arguments du type récusif tree dans ak attendent un valeur de type unit, et sont inutiles. Ils peuvent être supprimés et l'arité de ak décroît d'autant.

Des variations sont possibles selon l'ordre d'évaluation des appels récursifs. Évidemment les ak ne sont utiles que pour leurs effets de bord, donc l'ordre d'évaluation est primordiale. (Le plus couremment utilisé étant un parcours en profondeur, de gauche à droite).

Inversement, l'orde de calcul d'un fold peut ne pas être spécifié, (c'est le cas en Ocaml) car en général un fold n'est pas (ne doit pas) être utilisé pour faire des effets de bords.

Généralization


À tous les types

La démarche s'applique également aux types mutuellement récursifs.

Les types sont construits en combinant des déclarations de types somme, enregistrements, et des types de bases (entier, tuples, etc.).

On sait donc construire des fonctions de repliage (fold) de façon systématique pour tous les types déclarés.

À d'autres fonctions

Le cas de la fonction fold est assez général et le plus fréquemment utilisé.

Nous avons montré des sous cas de la fonction fold.

Ils existent d'autres formes qui ne correspondent pas à fold (e.g. itération) notemment pour des parcours d'arbres dans un ordre différent.

Cas général


Question

Peut-on programmer des fonctions telles fold une fois pour toute, par filtrage sur la structure du type de l'argument, puis en obtenir automatique des versions spécialisés pour chaque type?

Réponse

C'est ce qu'on appelle la programmation polytypique.

Difficultés
    ·Essentiellement de typage.
    ·Ce sont des travaux en cours de recherche...
    ·À la rigueur, on pourrait fournir quelques fonctions polytypiques primitives, sans permettre à l'utilisateur d'en programmer de nouvelles

(i.e. générer automatiquement les fonctions de repliage).


En pratique


Structuration du code Même sans support de la part du langage hôte, le programmation polytypique peut aider à structurer le code en séparant ce qui est
    ·ce qui est essentiel, que l'utilisateur devra impérativement fournir
    ·ce qui est secondaire, qui pourrait être déduit automatiquement de la structure des types (même, si le programmeur doit encore l'écrire manuellement).


Techniques et outils

En pratique, cela passe souvent par la séparation d'un type (trop) concret en
    ·en types abstraits.

    ·types concrets paramétrés.


Schématiquement

On veut implémenter une opération conséquence sur une structure.
  1. On sépare la partie essentielle de cette structure (serveur) de la partie secondaire (client)
  2. Le serveur ne doit pas dépendre de la partie secondaire
        ·soit il l'importe de façon abstraite
        ·soit il est paramétrique (polymorphe) par rapport à celle-ci.
  3. Le client founit au serveur une version particulière de cette sous-structure, en passant au serveurs les opérations manipulant la sous-structure.
  4. Ces fonctions sont écrire à la main mais de façon quasi-automatique.
  5. Une modification du client est facile. (Il faut simplement redéfinir les fonctions de manipulation de la structure secondaire).
On peut utiliser un foncteur pour le code essentielle (serveur). Au final, on a écrit une librairie...

Expressions arithmétiques avec variables

C'est une exemple concret

Représentation directe et aplatie
type exp =
  | Var of string
  | Int of int
  | Plus of exp * exp

let rec eval env = function
  | Var x -> List.assoc x env
  | Int n -> n
  | Plus (e1, e2) -> eval env e1 + eval env e2;;

Approche plus générique


Utilisation de fonctionnelles
Exercise 1   Donner la fonction exp_fold.
Answer
Montrer que eval peut s'exprimer à l'aide de exp_fold.
Answer
Donner une version de exp_fold avec arguments étiquetés permettant d'éviter tout confusion. Comparer avec l'écriture directe.
Answer

Calcul des variables d'un terme



Calcul direct
let rec vars =
  function
    | Var x -> [ x ]
    | Int n -> []
    | Plus (e1, e2) ->
        vars e1 @ vars e2;;
 

Calcul avec fold
let vars =
  exp_fold
    ~var:(fun x -> [ x ])
    ~int:(fun n -> [])
    ~plus:(fun ve1 ve2 ->
       ve1 @ ve2);;
Exemple
let e = Plus (Var "x", Plus (Var "y", Int 0))
let test = vars e;;
val test : string list = ["x"; "y"]
    ·Le schéma de récursion est pris en compte par exp_fold, ce qui n'est pas le cas pour le pattern matching.
    ·En contrepartie, le pattern matching est plus géneral: il peut se faire en profondeur, ne pas considérer tous les cas, etc.


Séparation des concepts


Variations sur la structure de donnée

On peut envisager les modifications suivantes.
    ·Ajout d'un noeud Times of exp *exp
    ·Renommage du constructeur Times en Produit
    ·Ajout d'un noeud Sigma of explist


Invariants

Dans tous ces cas, le calcul des variables est identique, peu importe la structure du terme sous-jacente. Il faut simplement collecter les variables en descendant récursivement dans la structure.

Séparation de la structure de termes

On décrit d'abord la structure de terme (ouverte) sans variable.
    type 'a sexp = Int of int | Plus of 'a * 'a;;
Puis la structure récursive avec variables pour une structure de termes donnée.
    type exp = Var of string | S of exp sexp;;


Code plus modulaire
let subexps = function
    Int _ -> []
  | Plus (e1,e2) -> [e1; e2]

let rec vars = function
  | Var x -> [ x ]
  | S s -> List.flatten (List.map vars (subexps s));;
Exercise 2   Donner la fonction de repliage sexp_fold.
Answer
Le traitement du constructeur S dans la fonction exp_fold est plus difficile. Il est de type exp sexp ->sexp, donc la récursion se passe sous le constructeur de type sexp. Donner une version exp_sexp_fold de type:
  var:(string -> 'a) ->  s:('b -> 'a) ->
    int:(int -> 'b) -> plus:('a -> 'a -> 'b) ->
      exp -> 'a
qui remplace dans son argument les noeuds de l'arbre par les fonctions correspondantes.
Answer
Définir une fonction ``naturelle'' sexp_map_fold de type
  int:(int -> 'a) -> plus:('b -> 'b -> 'a) ->
  f:('c -> 'b) -> 'c sexp -> 'a
qui prend un argument supplémentaire (par rapport à exp_fold) pour transformer les arbres du type paramètrique. En particulier, on devra retrouver les fonctions spécialisées exp_fold et exp_map en passant l'identité pour l'argument de nom f ou les constructeurs Int et Plus pour les arguments de nom int et plus.
Answer
En déduire une écriture plus simple de exp_sexp_fold.
Answer
Écrire la fonction vars à l'aide de exp_sexp_fold.
Answer

Robustesse par rapport aux variations

Une variation de structure ne nécessite que le changement de la fonction subterms. Par exemple,
type 'a sexp =
    Int of int | Sigma of 'a list | Prod of 'a list
let subexps = function
  | Int _ -> []
  | Sigma l -> l
  | Prod l -> l;;
    ·Les autres fonctions sont inchangées
    ·Toutefois, elle doivent être réévaluées, car sexp a changé
    ·Utilisation d'un foncteur pour partager la partie commune.


Fonctorisation


Expressions avec variables à partir de leur forme aplatie
module V0 = struct
  module type Sexp =
    sig
      type 'a t
      val subexps : 'a t -> 'a list
    end
  module Exp (S : Sexp) =
    struct
      type 'a sexp = 'a S.t
      type t = Var of string | S of t sexp
      let rec vars = function
        | Var x -> [ x ]
        | S s -> List.flatten (List.map vars (S.subexps s))
    end;;


La partie aplatie (suite)
  module  S =
    struct
      type 'a t = Int of int | Plus of 'a * 'a
      let subexps = function
          Int _ -> []
        | Plus (e1, e2) -> [e1; e2]
    end
end;;
module E = V0.Exp(V0.S)
open V0.S open E
let e = S(Plus (Var "x", S(Plus (Var "y", S(Int 1)))));;
let _ = vars e;;

Ajout d'une fonction d'évaluation


Enrichissement du foncteur
module V1 = struct
  module type Sexp =
    sig
      include V0.Sexp
      val eval : ('a -> int) -> 'a t -> int
    end
  module Exp (S : Sexp) =
    struct
      module Exp0 = V0.Exp (S)
      include Exp0
      let rec eval env = function
        | Var x -> List.assoc x env
        | S s -> S.eval (eval env) s
    end;;


Enrichissement de la structure
  module S1 =
    struct
      include V0.S
      let eval f =  function
          Int n -> n
        | Plus (e1, e2) -> f e1 + f e2
    end
end;;


Test
module Exp1 = V1.Exp(V1.S1)
open V1.S1 open Exp1
let e = S(Plus (Var "x", S(Plus (Var "y", S(Int 1)))))
let _ = eval ["x", 10; "y", 20] e;;
Ajout d'une fonction d'évaluation


Ajout à la structure (revient à une modification)
module S1' = struct
  type 'a t =
      Int of int | Sigma of 'a list | Prod of 'a list
  let subexps = function
    | Int n -> []
    | Sigma l -> l
    | Prod l -> l
  let eval f = function
    | Int n -> n
    | Sigma vl -> List.fold_left ( + ) 0 (List.map f vl)
    | Prod vl -> List.fold_left ( * ) 1 (List.map f vl)
end;;
module E1' = V1.Exp(S1');;
Applications


Exemples
    ·Un évaluateur, en séparant la structure de varriable et la gestion de l'environnement des autres concepts (primitives et leur évaluation).
    ·On peut de façon similaire écrire un algorithme d'unification abstrait par rapport à la structure de terme.


Avantages
    ·On peut facilement modifier la structure des termes sans avoir à réécrire l'algorithme d'unification.
    ·Les termes abstraits (vus par l'algorithme d'unification) ne voient pas leur implémentation concrète: un symbol (abstrait) peut être représenté par plusieurs noeud (concrets).


Conclusions


On retrouve un mélange de motifs connus

Sujet-observateur ou motif en peigne:
    ·Le type exp est casé en type 'asexp et la partie récursive
    ·On peut modifier indépendemment les deux parties de la structures, sans dépendre ni affecter l'autre
    ·On doit assembler les deux structures avant de les utiliser.
    ·Une fois assemblées les structures ne sont plus modifiables motif


Programmation polytypique

En séparant dans structure de donnée les parties essentielles des parties secondaires:
    ·Les détails sont séparés du code principale,
    ·Cela rends le code principal plus lisible, plus réutilisable,
    ·Les détails deviennet réguliers et pourraient (à l'avenir) être générés mécaniquement


Exercise 3  [Rammassage efficace]   Quel est la complexité de la fonction vars ci-dessus?
Answer
Donner une implémentation directe de vars de complexité linéaire (on ramassera les variables dans une liste qu'on passe de noeud en noeud.
Answer
Montrer que l'on peut écrire une version analogue de vars à partir de la fontion exp_fold.
Answer

Exercise 4  [Unification]   Implémenter un algorithme d'unification en séparant la représentaion concrète des termes de la structure de termes

Donner deux instances de l'algorithme d'unification, par exemple, l'un minimal avec une structure de termes comprennat seulement un symbol d'arité deux et un symbol constant, l'autre comprenant en plus un symbol d'arité variable.

This document was translated from LATEX by HEVEA and HACHA.