Graphe d'interférence

1 Environnement

Comme d'habitude, récupérer l'archive zyval.tar, la décompacter, et écrire l'implémentation manquante liveness.ml à partir de squelette.ml. Soit comme d'habitude :

Récupérer zyval.tar et squelette.ml.

Mettre en place.

# tar xf zyval.tar
# cp squelette.ml zyval/liveness.ml
# cd zyval
# make depend
# make

Au passage, il y a encore des élèves qui ne recompilent pas fréquement où qui répugnent à utiliser make. Je trouve cela à peine croyable.

2 Description du squelette

Le travail pratique de cette semaine se décompose naturellement en deux : d'abord calculer le graphe de flot, ensuite en déduire le graphe d'interférence. Cela est exprimé clairement par les deux points d'entrée principaux décrits dans liveness.mli :

val flow : instr list -> flowinstr list val interference : flowinstr list -> igraph

On remaquera que la fonction flow ne produit pas exactement un graphe de flot, mais plutôt une liste d'instructions décorées par des informations de liveness (type flowinstr nous y reviendrons).

3 Calcul des temporaires vivants

3.1 Ce qu'il faut faire

Compte tenu du temps qui nous est imparti, le travail pratique est assez limité, ce qui est bien domage. Le code donné fait déjà presque tout le travail. Voici donc la fonction flow.

let flow code = let g = mk_graph code in let niters = fixpoint g in if !verbose then begin prerr_endline ("Graphe de flot calculé en "^string_of_int niters^" itérations") end ; (* C'est le résultat *) graph_to_flowinstrs g

Sont déjà réalisés, le calcul du graphe de flot décoré par les Def et les Use (c'est la fonction mk_graph, notons tout de même que nous avons déjà calculé un graphe de flot à l'occasion de l'optimisation du contrôle) et la transformation du graphe en liste d'instructions décorées par les informations de liveness (c'est la fonction graph_to_flow_instr).

Reste donc à réaliser la fonction fixpoint qui calcule les Out et les In. Son type est le suivant :

val fixpoint : val fixpoint : flowinfo Graph.t -> int

Cette fonction prend en argument un graphe orienté (type générique 'a Graph.t) dont les sommets sont décorés par diverse informations pertinentes (type flowinfo).

type flowinfo = { instr : Ass.instr ; (* Une instruction *) (* Comportement de l'instruction *) def : temp set; (* Écrits par l'instruction Def *) use : temp set; (* Lus par l'instruction Use *) (* Temporaires vivants *) mutable live_in : temp set; (* En entrée In *) mutable live_out : temp set; (* À la sortie Out *) }

Les sommets du graphe passé en argument à la fonction fixpoint sont déjà décorés par toutes les informations non mutables (c'est à dire instr, def, use). La mission de la fonction fixpoint est de calculer les informations mutables (c'est à dire live_in et live_out) ou autrement dit les ensembles de temporaires vivants en entrée et en sortie de l'instruction considérée. On notera que les ensembles de temporaires sont réalisés à l'aide du module Smallset.

3.2 Repère de réussite

Pour vérifier que vous avez réussi le travail pratique, vous disposez de deux moyens.

L'examen visuel de la sortie de zyval.
L'examen visuel des graphes d'interférence produits (car le squelette calcule aussi les graphes d'interférence).

Ces examens visuels se feront en passant à zyval une option (par exemple « -4 ») qui restreint fortement les registres de la machine utilsables par le compilateur, ce qui permet justement l'examen.

Prenons un premier exemple : le programme factrec.p de factorielle récursive. Dans l'état actuel du programme (fonction fixpoint qui ne fait rien). On a :

# ./zyval -4 factrec.p
*** Graphe de flot ***
fact:   # <=    # 
    subu $sp, $sp, fact_f       # <=    # 
    move $113, $ra      # $113 <= $ra   # 
    move $112, $s0      # $112 <= $s0   # 
    move $108, $a0      # $108 <= $a0   # 
    li   $114, 1        # $114 <=       # 
    ble  $108, $114, L12        # <= $108 $114  # 
L13:    # <=    # 
    sub  $a0, $108, 1   # $a0 <= $108   # 
    jal  fact   # $v0 $a0 $ra <= $a0    # 
    move $109, $v0      # $109 <= $v0   # 
    mul  $107, $108, $109       # $107 <= $108 $109     # 
    b    fact_end       # <=    # 
L12:    # <=    # 
    li   $107, 1        # $107 <=       # 
fact_end:       # <=    # 
    move $v0, $107      # $v0 <= $107   # 
    move $ra, $113      # $ra <= $113   # 
    move $s0, $112      # $s0 <= $112   # 
    addu $sp, $sp, fact_f       # <=    # 
    j    $ra    # <= $v0 $s0 $ra        #

Chaque instruction est suivie des temporaires définis et utilisés (sous la forme # Def<= Use, remarquez au passages les Def et les Use de l'appel de fonction et de l'instruction de retour). Ensuite viennent les Out, ici vides.

Une fois écrite la fonction fixpoint on obtient normalement :

# ./zyval -4 factrec.p
*** Graphe de flot ***
fact: # <=  # $a0 $s0 $ra 
    subu $sp, $sp, fact_f # <=  # $a0 $s0 $ra 
    move $113, $ra # $113 <= $ra  # $a0 $s0 $113 
    move $112, $s0 # $112 <= $s0  # $a0 $112 $113 
    move $108, $a0 # $108 <= $a0  # $108 $112 $113 
    li   $114, 1 # $114 <=  # $108 $112 $113 $114 
    ble  $108, $114, L12 # <= $108 $114  # $108 $112 $113 
L13: # <=  # $108 $112 $113 
    sub  $a0, $108, 1 # $a0 <= $108  # $a0 $108 $112 $113 
    jal  fact # $v0 $a0 $ra <= $a0  # $v0 $108 $112 $113 
    move $109, $v0 # $109 <= $v0  # $108 $109 $112 $113 
    mul  $107, $108, $109 # $107 <= $108 $109  # $107 $112 $113 
    b    fact_end # <=  # $107 $112 $113 
L12: # <=  # $112 $113 
    li   $107, 1 # $107 <=  # $107 $112 $113 
fact_end: # <=  # $107 $112 $113 
    move $v0, $107 # $v0 <= $107  # $v0 $112 $113 
    move $ra, $113 # $ra <= $113  # $v0 $ra $112 
    move $s0, $112 # $s0 <= $112  # $v0 $s0 $ra 
    addu $sp, $sp, fact_f # <=  # $v0 $s0 $ra 
    j    $ra # <= $v0 $s0 $ra  #

En regardant bien on note que les temporaires de sauvegardes des callee-saves, 112 et 113 sont vivants à travers toute la fonction (mais pas à la sortie, à cause des Use de l'instruction de retour). On note aussi que la durée de vie de temporaires « auxiliaires » (par exemple 114) est bien courte. Enfin, la fonction lit bien son argument dans a0, comme il est visible en considérant les Out de son étiquette d'entrée.

Mais bon, pour vérifier que votre programme passe le test, vous pouvez plutôt laisser la commande diff comparer sa sortie avec une sortie de référence factrec-live.txt :

# ./zyval -4 factrec.p > a
# diff a factrec-live.txt

Ou mieux encore :

# ./zyval -4 factrec.p | diff - factrec-live.txt

Il ne doit rien se passer.

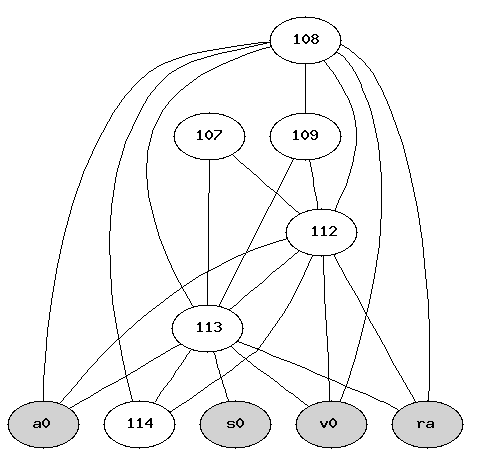
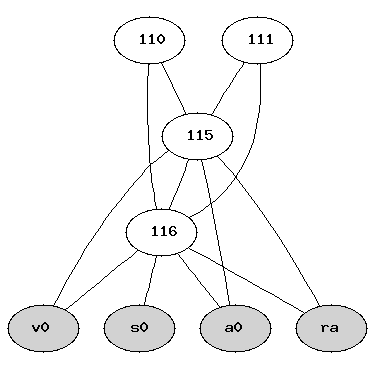
Voici, un second exemple, la factorielle itérative factiter.p et sa sortie de référence factiter-live.txt (toujours avec l'option « -4 »).

Un autre moyen de vérifier la correction de votre programme est d'examiner les graphes d'interférence produits. La commande « ./zyval -4 factrec.p » produit le grephe d'interférence des fonctions fact et main de ce programme sous la forme de deux fichiers factrec-fact.ig et factrec-main.ig visualisable par la combinaison des commandes dot et kghostview. Soit par exemple pour la factorielle récursive factrec.p :

# ./zyval -4 factrec.p
# dot -Tps factrec-fact.ig > fact.ps
# dot -Tps factrec-main.ig > main.ps
# kghostview fact.ps & kghostview main.ps &
#

On a ces deux jolis dessins :

À gauche le graphe d'inteférence de la fonction fact, à droite celui de la fonction main. Dans le graphe de fact on constate par exemple que le temporaire argument 108 interfère avec beaucoup de temporaires, y compris trois des quatre registres machines disponibles.

La même manip sur la factorielle itérative factiter.p nous donne :

C'est le graphe d'inteférence de la fonction fact itérative, celui de la fonction main ne change pas. On remarque par exemple que 108 n'interfère plus avec aucun registre machine. La différence avec le cas précédent de la factorielle récursive provient bien entendu de l'appel récursif qui détruit a0, v0 et ra en pleine durée de vie de 108.

3.3 Allez-y

Donc il faut écrire le code de fixpoint. On notera que cette fonction renvoie un entier qui est le nombre d'itérations effectuées. Voici un rappel de quelques informations utiles.

Description des ensembles de temporaires Smallset.
Description des graphes de flot.
L'algorithme à utiliser en pratique pour calculer les live-in et les live-out. On notera :
- La boucle de 1 à n est à comprendre comme une boucle « pour tous les sommets du graphe de flot », (cf. Graph.iter, ou encore donnez-vous une liste explicite de tous les sommets du graphe de flot, par la fonction Graph.nodes).
- Dans l'algorithme informel, Out est noté Speed et In n'apparaît pas explicitement. Rapellons aussi les equations « définition » des In et des Out.
  
  In(i) = Use(i) ∪ ( Out(i) \ Def (i)) Out (i) =
  
  ∪
  
  j ∈ Succ(i)
  In(j)

Voir la solution si besoin.

4 Graphe des interférences

4.1 Ce qu'il faut faire

La fonction interference du squelette calcule déja le graphe des interférences. L'exercice consiste à ajouter dans ce graphe les arcs « moves » qui indiquent des relation d'affinités entre temporaires. Par contraste, les arcs d'interférence indiquent une relation d'incompatibilité. Au sens que l'on aimerait bien que deux temporaires reliés par un arc « move » occupent au final le même registre, tandis que deux temporaires reliés par un arc « d'interférence » ne peuvent pas occuper au final le même registre.

Pour toute paire de temporaires t₁ × t₂ on définit la relation d'affinité ainsi :

Il y a une instruction de transfert (un move) entre les temporaires t₁ et t₂ dans le code.
Il existe un troisième temporaire t₃ avec lequel t₁ et t₂ se sentent des affinités.

Autrement dit, on fabrique d'abord les arcs move entre temporaires directement reliés par des instructions de transfert, puis on effectue la fermeture transitive de cette relation.

En fait, il convient de hiérachiser un peu les préférences. La relation d'affinité signifie que deux temporaires aimeraient bien occuper le même registre (parce qu'il y un transfert entre eux). Or il est clair que :

Il ne sert à rien d'envisager une affinité entre deux temporaires qui interfèrent.
Une chaîne de transferts qui passe par un vrai registre (ou plus) n'a pas trop d'intérêt. En effet, supposons que le code contient par exemple les transferts t₁ ← r₁ , t₁ ← t₂, t₂ ← r₂, t₃ ← r₂. Alors on a la chaîne de transferts :
r₁ ↔ t₁ ↔ t₂ ↔ r₂ ↔ t₃
Mais il n'y a clairement aucun intérêt à envisager de ranger t₃ dans r₁, ou plus genéralement à ranger t₃ et t₁ (ou même t₂ si le registre n'est pas r₂) dans le même registre : on economisera aucun transfert.

On souhaite donc limiter les affinités, on peut par exemple proposer la relation suivante d'affinité selective, definie entre les temporaires t₁ et t₂ par :

Il existe, entre t₁ et t₂, une chaîne de transferts n'impliquant que de vrais temporaires (et non des registres).
Les temporaires t₁ et t₂ n'interfèrent pas.

Cela revient à considérer d'abord les transferts entre temporaires qui n'interfèrent pas, puis à opérer une fermeture transitive un peu spéciale qui évite de traverser les registres.

Je vous conseille de commencer par la relation d'affinité généralisée, puis éventuellement de modifier un peu votre code pour fabriquer la relation d'affinité sélective.

4.2 En pratique

Examinons un peu la fonction interference son argument et son résultat :

val interference : flowinstr list -> igraph

L'argument est la liste des instructions du corps d'une fonction augmentées des informations de liveness pertinentes pour le calcul des interférences. Ces informations sont les Def, les Use et les Out.

type flowinstr = {finstr:Ass.instr ; fdef: Gen.temp set ; fuse : Gen.temp set ; fout : Gen.temp set}

Il n'y a aucun mystère ici, la liste des flowinstr est facilement produite à partir du graphe de flot complet de la question précédent simplement (par la fonction graph_to_flowinstrs) en oubliant les informations devenues inutiles, c'est à dire la structure même du contrôle et les In.

Le graphe d'interférence (type igraph) est un graphe non-orienté (type générique ('a, 'b) Sgraph.t) dont les sommets (type interference) sont des temporaires et les arcs (type ilab sont de deux catégories : arcs d'interférence et d'affinité).

(* Sommets du graphe d'interférence *) type interference = { temp : temp; (* Les champs suivants sont utiles pour l'allocation de registres *) mutable color : temp option ; mutable occurs : int ; mutable degree : int ; mutable elem : ((interference Sgraph.node) Partition.elem) option ; } (* Les deux sortes d'arcs *) type ilab = Inter | Move_related type igraph = (interference, ilab) Sgraph.t

On notera bien que seul nous intéresse pour le moment le champ temp des sommets.

Pour mieux comprendre, voici la construction du graphe d'interférence proprement dit. Dans toute la fonction interference le graphe construit est dans la variable ig et sera construit par des appels aux fonctions du module Sgraph des graphes non-orientés. Le graphe est créé vide initialement :

let interference code = let ig = Sgraph.create ibidon in …

On se donner d'abord une fonction utilitaire qui à un temporaire associe un sommet du graphe, il est important d'associer au plus un sommet à tout temporaire, on se débrouille avec une table de hachage (module Hashtbl de la libraire standard) :

(* Besoin d'une association temporaire -> sommet *) let temp2nodes = Hashtbl.create 17 in let get_node r = try Hashtbl.find temp2nodes r with | Not_found -> let n = Sgraph.new_node ig (mk_info r) in Hashtbl.add temp2nodes r n ; n in …

Il est pratique de disposer d'une petite fonction qui prend en argument deux sommets du graphe et ajoute un arc (de nature k qui peut être Inter ou Move_related) entre les deux sommets. Aucun arc entre registres n'est fabriqué, car l'allocation de registres se passe de cette information sans intérêt (deux registres de toute façon interfèrent toujours).

let mk_edge n1 n2 k = let r1 = (Sgraph.info ig n1).temp and r2 = (Sgraph.info ig n2).temp in if not (mem r1 registers) || not (mem r2 registers) then Sgraph.new_edge ig n1 n2 k in …

Étant donné une instruction décorée i, on peut maintenant construire les sommets et les arcs d'interférence par elle enegendrés :

(* Fabrication du graphe d'interférence proprement dit *) let step_instr i = match i.finstr with | Move (_,_,_) -> Smallset.iter i.fdef (fun d -> let nd = get_node d in Smallset.iter (Smallset.diff i.fout i.fuse) (fun r -> mk_edge (get_node r) nd Inter)) | _ -> Smallset.iter i.fdef (fun d -> let nd = get_node d in Smallset.iter i.fout (fun r -> mk_edge nd (get_node r) Inter)) in

La fonction suit directement les définitions du poly (c'est a dire que les temporaires vivants en sortie d'une instruction interfère avec ses Def) en distingant le cas particulier des instructions de transfert (où il n'y pas lieu d'enregistrer une interférence entre un Def et un Use qui peuvent bien occuper le même registre, au vu de cette seule instruction de transfert). On notera que la fonction iter ci dessus est l'itération sur tous les éléments d'un ensemble de temporaires (module Smallset).

Bon, nous somme maintenant bien équipés pour construire notre graphe d'interférence : il suffit d'appliquer step_instr à toutes les instructions du code passé en argument. Pour des raisons esthétiques on s'assure aussi que tous les registres de la machine sont bien mis dans le graphe.

(* Un sommet par registre machine *) Smallset.iter registers (fun r -> ignore (get_node r)) ; (* Pour toutes les instructions... *) List.iter step_instr code ;

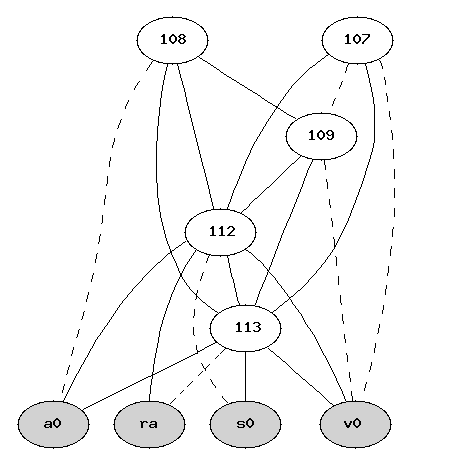
C'est maintenant à vous de jouer : ajouter les arcs d'affinité (Move_related) au graphe ig. C'est à dire :

En un parcours du code ajouter les arcs correspondant aux transferts immédiats entre temporaires.
Calculer la fermeture transitives des arcs Move_related.

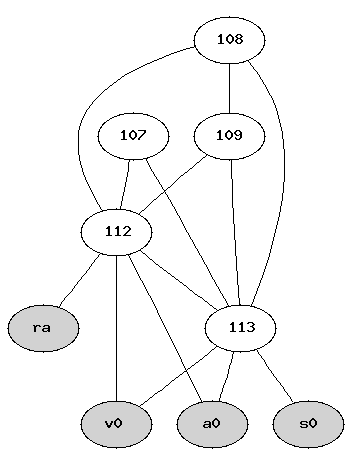
Vous pourrez contempler vous résultats comme précedamment (les arcs Move_related sont indiqués en pointillés dans les dessins).

Par exemple :

# ./zyval -4 factiter.p
# dot -Tps factiter-fact.ig > fact.ps
# kghostview fact.ps

donnera ce joli dessin.

Voir la solution si besoin.

5 Complément

Changer l'ordre de parcours, les noeuds du graphe de flot. Essayer d'abord le plus mauvais parcours possible, puis le parcours selon un ordre quasi-topologique.
Calculer les durées de vie sur un graphe des blocs de base. Estimer le gain en vitesse sur les exemples les plus difficiles, par exemple test/bignum.p.

Ce document a été traduit de L^AT_EX par H^EV^EA.