La duchesse de Valombreuse est chargée de dresser le plan des tables du dîner annuel de l'amicale du club de polo de Lyons-la-forêt. La duchesse souhaite faire du dîner le succès majeur de la saison, mais les membres de l'amicale ne s'entendent pas forcément très bien entre eux. La duchesse a donc demandé discrètement à chaque membre de l'amicale la liste de ceux qu'il ne souhaite pas voir à sa table. Elle est dépassée par le reste de sa tâche. Elle vous demande (car vous vous êtes imprudemment promené à Lyons en grand-uniforme !) de dresser le plan du dîner.
Afin de préserver la quiétude de la vie mondaine de Lyons-la-forêt, la duchesse a identifié chacun des membres de l'amicale par un entier entre 0 et n−1. Elle vous donne ensuite l'état des relations sociales sous la forme d'un fichier texte.
'\n' ».':' »,',' » et terminée par le caractère retour à la ligne
« '\n' ». Cette suite peut être vide.Par exemple, voici une liste possible.
4 0:1,2 3: 1:0,3 2:3
Question 1.
Cette
question demande diverses expressions régulières. On utilisera
impérativement la syntaxe suivante : les motifs caractères sont
donnés en syntaxe Java ('0', '1', …,
':', '\n', etc.), le motif vide est noté є,
la séquence par la juxtaposition E1 E2, l'alternative par
l'opérateur binaire E1 ∣ E2, la répétition par l'étoile
E⋆, et on utilise systématiquement les parenthèses pour
lever les ambiguïtés. Une fois nommée une expression régulière, on
pourra utiliser son nom à la place de celle-ci.
a)
Donner l'expression régulière D qui décrit un chiffre, puis
l'expression régulière I qui décrit l'écriture en base 10 d'un
entier positif ou nul.
Si on souhaite éviter les zéro initiaux inutiles, ce qui n'est pas l'usage en informatique, on écrira plutôt :
Note : Une erreur fréquente a été de poser I = (D)⋆, qui ne convient pas, puisque le mot vide n'est pas l'écriture d'un entier.
b) Donner l'expression régulière L qui décrit les lignes du fichier à partir de la seconde.
Note : Le nombre de copies où j'ai trouvé D à la place de I dans les sous-questions b) et c) est proprement incroyable (non-sanctionné).
c) Donner l'expression régulière F qui décrit le fichier de la duchesse.
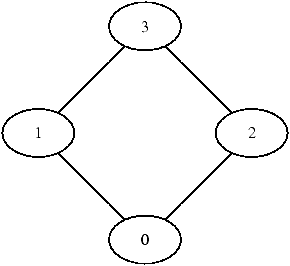
Que le membre i refuse de dîner avec j ou que le membre j refuse de dîner avec i conduit au même résultat : les membres i et j ne peuvent pas dîner à la même table. Pour organiser le dîner, on introduit un graphe (non-orienté) (S, A), dont l'ensemble des sommets S est 0, 1, …, n−1 et l'ensemble des arêtes est l'ensemble des ensembles de la forme {i, j}, tels que i et j ne peuvent pas dîner à la même table. Par exemple, pour la liste de la duchesse déjà donnée, le graphe est donné par la figure 1.
Il est important de remarquer que les arêtes sont ici des ensembles de deux sommets. C'est-à-dire qu'il existe au plus une arête entre deux sommets distincts et qu'il n'y a pas d'arête reliant un sommet à lui même — ce qui est logique un membre de l'amicale qui refuse de s'asseoir à la même table que lui-même ne viendra pas au dîner. On notera une arête entre deux sommets s0 et s1, indifféremment comme s0 ↔ s1 ou s1 ↔ s0.
Les graphes sont représentés par des objets de la classe Graphe,
partiellement spécifiée ci-dessous :
Question 2.
La liste de la duchesse est maintenant disponible en machine sous la
forme d'un tableau t de tableaux d'entiers.
Le tableau t est de taille n et chacun de ses
éléments t[i] est un tableau qui regroupe
ceux avec qui i refuse de dîner.
Ainsi, dans le cas de notre exemple, t[0] est le tableau
{1, 2}, t[1] est le tableau {0, 3},
t[2] est le tableau {3},
et t[3] est le tableau vide {}.
Écrire la méthode static Graphe fabriquer(int [] [] t) qui prend
le tableau t en argument et renvoie le graphe correspondant.
Attention : Il faut créer une arête donnée i ↔ j au plus une
fois, sachant bien que les notations i ↔ j et j ↔ i
représentent la même arête.
mat du graphe. Comme le
graphe est non-orienté, cette matrice est symétrique.
Dans cette représentation matricielle, le fameux g.existeArc(i,j)
manquant correspond exactement au test mat[i][j].Note : Cette question a souvent été ratée. Il fallait bien voir que…
new boolean[n][n] valent false, car la norme de Java le
spécifie. Je dirais même que c'est une bonne pratique que de
s'appuyer sur la norme.
t[i] est un tableau, dont la taille
est t[i].length et dont un élément est
t[i][k] — à lire comme
(t[i])[k].Et d'ailleurs, en Java, une « matrice » est toujours un tableau de tableaux. Écrire par exemple new boolean[n][n] le cache un peu. Mais en fait,
ce constructeur
false.
{} n'est pas null, mais un tableau dont la taille est zéro.
t[i] (k ici) a remplacé
la valeur (t[i][k] ici). Le code, en posant
j = t[i][k] évite de répéter quatre fois t[i][k], et
surtout, il rend l'erreur moins probable.
existeArc. Si on en voulait
absolument une, on pouvait la programmer (avec la méthode
voisins présentée plus tard, il est vrai).
g.ajouterArc(s0,s1) construit
une arête dans un graphe non-orienté1.
La matrice mat, qui reflète le graphe partiellement construit
doit être symétrique.
Certaines copies font usage de la boucle for améliorée, les risques
d'erreurs entre k et t[i][k] sont alors réduits à néant.
L'organisation du dîner revient à affecter chaque membre de l'amicale à une table, de sorte que deux convives qui refusent de dîner ensemble sont assis à des tables différentes. Il s'agit exactement du problème de coloriage de graphe, associer une couleur à chaque sommet du graphe, de sorte que, pour toute arête s0 ↔ s1, les couleurs associées à s0 et s1 sont distinctes.
Évidement, organiser le dîner est possible : chacun peut manger seul. Mais la convivialité risque d'en souffrir. On cherche à faire mieux avec l'algorithme glouton qui colorie les sommets du graphe dans l'ordre 0, 1, …, n−1. Les couleurs sont représentées par des entiers, 0, 1, etc. Pour colorier le sommet i, on choisit la plus petite couleur possible qui est compatible avec les couleurs des voisins de i qui sont déjà coloriés.
Question 3. Colorier le graphe de la figure 2 à la main selon l'approche gloutonne. Le plus simple est de redessiner le graphe colorié (avec des hachures ou des crayons de couleurs).
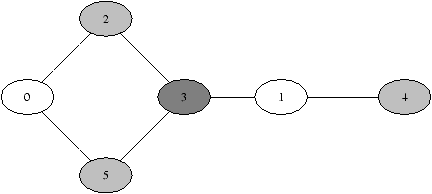
Note : Il n'est peut-être pas inutile de préciser le déroulement du coloriage :
| sommet | voisins[couleur] | couleur allouée | ||
| 0 | 2[], 5[] | 0 | ||
| 1 | 3[], 4[] | 0 | ||
| 2 | 0[0], 3[] | 1 | ||
| 3 | 1[0], 2[1], 5[] | 2 | ||
| 4 | 1[0] | 1 | ||
| 5 | 0[0], 3[2] | 1 | ||
La classe Graphe possède une méthode voisins spécifiée
ainsi :
L'appel voisins(s) renvoie donc les
sommets v du graphe tels qu'il existe une arête s ↔ v,
sous la forme d'un objet qui implémente l'interface
Iterable<Integer>. Ce qui veut simplement dire que l'on peut
parcourir les voisins2
d'un sommet s par la construction for.
Par exemple, voici comment on peut afficher les voisins d'un sommet
donné s :
Question 4.
Compléter la classe Graphe
par une méthode
int [] glouton() qui réalise l'algorithme glouton.
Le tableau d'entiers retourné par la méthode glouton indique les
couleurs affectées aux n sommets.
Note : Il y a deux difficultés :
j < i
donne une solution élégante.
impossible donne une solution
simple, mais qui conduit à une complexité quadratique. En effet,
allouer un tableau de taille n coûte de l'ordre de n
opérations (à cause de l'initialisation).
Une autre solution sans tableau, avec un usage relativement sûr et élégant des boucles :
Je trouve ces manips de variables booléennes assez
casse-cou. Utiliser return dans une méthode auxiliaire est
souvent plus sûr.
Question 5.
La duchesse
souhaite maximiser la convivialité,
c'est-à-dire que vous souhaitez minimiser le nombre de tables.
a)
Confirmer par un exemple que
l'algorithme glouton ne colorie pas les graphes avec le nombre minimal
de couleurs possible.
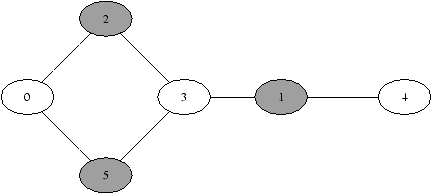
b) Un camarade vous suggère de commencer par placer les membres les plus exigeants, autrement dit de colorier les sommets du graphe dans l'ordre décroissant des degrés (le degré d'un sommet est le nombre d'arêtes issues du sommet). Quand vous lui demandez : mais comment départager deux sommets de même degré ? Il repond : dans ce cas, on fait ce que l'on veut, ça marchera toujours.
Montrer
lui que son astuce ne permet pas de colorier un graphe
arbitraire avec un nombre minimal de couleurs.
Indication : On pourra montrer que la suggestion du camarade
ne conduit pas au coloriage avec le moins de couleurs possibles d'un
graphe particulier, par exemple celui-ci.
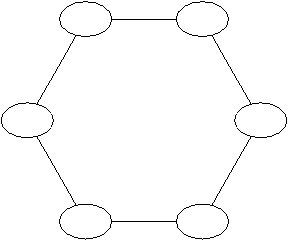
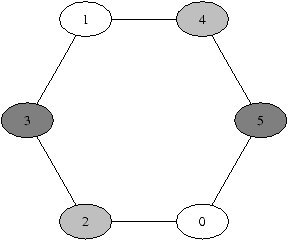
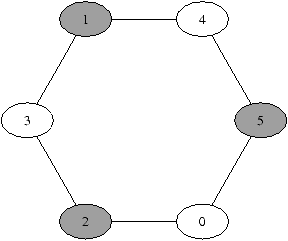
La duchesse vient de vous téléphoner pour vous signaler que le club-house ne possède que deux tables. La question posée devient donc : colorier un graphe avec deux couleurs.
Un chemin (élémentaire) de taille p (p ≥ 0), noté s0 ↔ s1 ↔ ⋯ ↔ sp, est défini comme une suite ordonnée de sommets deux à deux distincts s0, s1, …, sp tels que les arêtes s0 ↔ s1, …, sp−1 ↔ sp existent.
Un circuit (élémentaire) de taille p (p > 2), noté s0 ↔ s1 ↔ ⋯ ↔ sp−1 ↔ s0, est défini ainsi :
On note qu'une simple arête s0 ↔ s1 n'engendre pas de circuit s0 ↔ s1 ↔ s0, en vertu de la condition p > 2.
Question 6. Montrer qu'un graphe qui contient un circuit de taille impaire ne peut pas être colorié avec deux couleurs.
Note : C'est une fausse « preuve par l'absurde ». Il est plus élégant de formaliser différemment : un circuit 2-coloriable est nécessairement de taille paire. Soit donc un circuit 2-coloriable, et soit 0 la couleur de s0 (choix arbitraire). Pour tout k (0 ≤ k < p), en considérant le chemin s0 ↔ s1 ↔ ⋯ ↔ sk on voit que la couleur de sk est 0, si et seulement si k est pair, et 1 autrement. Par ailleurs, en raison de l'arête sp−1 ↔ s0, la couleur de sp−1 est 1. L'entier p−1 est donc nécessairement impair, c'est à dire que le circuit est de taille paire.
On peut voir un arbre comme un graphe particulier : il existe un sommet particulier (la racine), et pour tout sommet s il existe un unique chemin issu de la racine et aboutissant en s.
Question 7. Colorier un arbre avec deux couleurs.
Note : Le fait ci-dessus est « évident » : en gros deux sommets voisins dans un arbre sont en relation père–fils. On peut vouloir le montrer à partir de la définition des arbres de l'énoncé (cela n'a pas été jugé nécessaire lors de la correction). Soit donc une arête s ↔ v. Soient S et V, les chemins (uniques) de la racine à s et v respectivement. On va montrer que l'on a soit S = V ↔ s, soit V = S ↔ v. Supposons d'abord que V ↔ s est un chemin (c'est-à-dire supposons que s n'est pas un sommet de V), alors on peut conclure par l'unicité du chemin S. Sinon, s apparaît dans V, qui est donc de la forme V = V1 ↔ s ↔ V2. Par unicité de S, il vient V = S ↔ V2, ce qui entraîne que v n'apparaît pas dans dans S (sinon V contiendrait deux fois v). On peut alors conclure comme précédemment en inversant les rôles de s et de v.
Re-Note : Il me semble que dire « colorier les sommets de l'arbre avec la parité de leur profondeur » est suffisamment explicite. Par sécurité (mais on perd alors du temps) on peut vouloir donner un algorithme en pseudo-code ou en Java. Il convient alors d'être précis. Si on réutilise la structure de graphe de l'énoncé, il faut faire attention à ne pas boucler, car le père d'un sommet est bien un voisin de ses fils :
Si on utilise sa propre structure, il faut la définir, ou au moins faire comprendre au correcteur ce que l'on a voulu dire :
Question 8. En utilisant la notion d'arbre couvrant du cours, colorier un graphe connexe dont tous les circuits sont de taille paire, en utilisant deux couleurs.
Il reste à montrer que les arêtes de A ∖ T relient des sommets de couleurs différentes. Soit donc s0 ↔ s1 une telle arête. Il existe deux chemins C0 = r ↔ ⋯ ↔ s0 et C1 = r ↔ ⋯ ↔ s1 dont toutes les arêtes sont dans T. Les chemins C0 et C1, qui commencent par le même sommet admettent un plus grand préfixe commun P = r ↔ ⋯ ↔ a.
Note : Ici une preuve a été requise lors de la correction, car la 2-coloriabilité du graphe n'est pas évidente. En abusant des notations on peut se passer du deuxième cas ci-dessus.
Il y a une preuve plus élégante, ou plus exactement une organisation plus élégante des arguments de la preuve ci-dessus. Tout d'abord, l'existence d'un chemin élémentaire entre deux sommets quelconques d'un graphe connexe est facile à démontrer (par ex. en itérant le remplacement des circuits c ↔ ⋯ ↔ c par c dans un chemin quelconque). Par connexité du graphe, colorier l'un quelconque de ses arbres couvrants affecte une couleur à tous les sommets. Soit maintenant s0 ↔ s1 arête qui n'est pas une arête de l'arbre choisi. L'arbre couvrant est connexe (comme tous les arbres) il existe donc un chemin élémentaire de s0 à s1 dans l'arbre, qui devient un circuit élémentaire si on y ajoute l'arc s0 ↔ s1. Le circuit est par hypothèse de taille paire, le chemin (de l'arbre) est donc de taille impaire, ce qui entraîne que les couleurs de s0 et s1 sont distinctes.
En tout état de cause l'exercice de rédiger une preuve est délicat. Il convient de bien identifier ce qui doit être justifié. Par exemple à la question 6, une récurrence est exagérée. En revanche, dans cette question, il faut identifier le circuit élémentaire considéré.
Question 9.
Dans
cette question on suppose que le graphe this est connexe.
Ajouter une méthode int [] colorierDeuxConnexe() à la classe des
graphes, spécifiée ainsi :
this n'est pas coloriable avec deux couleurs,
alors la méthode renvoie null.
Indication : Un parcours de graphe construit un arbre couvrant.
vu, mais alors il faut initialiser
les cases de couleur à par exemple -1 et remplacer
le test de vu[s] par couleur[s] >= 0. Note : La solution exploite la question précédente. On colorie l'arbre couvrant du parcours. La correction du programme (preuve non-exigée) repose sur les observations suivantes :
Le parcours DFS peut aussi se programmer avec le test de vu[s]
avant les appels à dfs, ce qui est je crois la technique
du cours. Cela revient bien entendu au même. On peut d'ailleurs dans
ce cas économiser l'argument int coul.
Certains prenent au pied de la lettre la structure de l'énoncé, et procèdent ainsi :
Il faut alors écrire pas mal de code…
Question 10.
Même question que la précédente en ne supposant pas le
graphe this connexe.
Note : Quelques copies utilisent une exception pour
signaler les graphes non deux-coloriables.
Voici donc un nouveau DFS, écrit dans la classe Graphe.
Cela peut conduire à une solution particulièrement simple pour cette question, car dégagée de la nécessité de vérifier la valeur rendue par le parcours des composantes connexes.
Et pour la question 10, remplacer les deux lignes 4 et 5 par :
Graphe avec des listes de voisins, alors un appel à
ajouterArc modifie deux listes de façon interne. Mais il n'est
pas utile de le savoir.
This document was translated from LATEX by HEVEA.