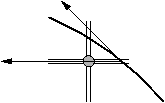
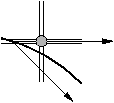
Soit donc le point (x0,y0) approximation, par le résultat précédent la courbe intersecte le segment unité centré en (x0,y0). On suppose que x0+1 appartient au domaine de f. Par hypothèse la courbe intersecte le segment unité centré en (x0,y0), et l'axe vertical x = x0+1 au point (x0+1, f(x0+1)).
D'après l'interprétation géométrique, on voit que l'intersection avec la verticale x = x0+1 se situe nécessairement dans l'un des deux segments unité centrés en (x0+1, y0) ou (x0+1, y0-1) (soit y0-3/2 ≤ f(x0+1) ≤ y0+1/2 en formules).
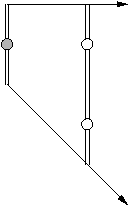
- Le domaine est limité au huitième de cercle compris entre le nord et le nord-est.
- Un premier point est connu : le point (0,R).
- Le test de choix entre (x0+1,y0) et (x0+1,y0-1) repose
sur la position du point
(x0+1,y0-1/2) soit sur le signe de
Si d est positive alors le point suivant est (x0+1,y0-1), sinon c'est (x0+1,y0).
d = (x0+1)2 + (y0- 1 2 ) - R2
|
static void cercle(int r) { int x = 0 ; int y = r ; while (x <= y) { pxl(x,y) ; double d = (x+1)*(x+1) + (y-0.5)*(y-0.5) - r*r ; x++ ; if (d > 0) { y-- ; } } } |
Par ailleurs pour x et y entiers, e = d-1/4 est entier et les signes de d et e sont identiques. La nullité de e entraînant d = 1/4> 0. (C'est-à-dire que le cas e = 0 est en fait d > 0). On peut donc recoder la méthode cercle ainsi :
|
static void cercle(int r) { int x = 0 ; int y = r ; int e = 1-r ; while (x <= y) { pxl(x,y) ; if (e >= 0) { y-- ; e -= 2*y ; } x++ ; e += 2*x+1 ; } } |
Enfin tous ces exemples semblent montrer que procéder à la marche du roi pour x0 ≤ y0 produit bien une approximation de Freeman, mais il faut le montrer !
On considère d'abord le cas où le dernier point allumé est de la forme (x0, x0+1). Par hypothèse le point (x0+1, x0+1) n'est pas allumé. Et donc le point milieu (x0+1, x0 + 1/2) est au dessus du cercle. Par symétrie selon la diagonale, le point (x0+1/2, x0 + 1) est également au dessus du cercle et le point (x0+1, x0+1) ne doit pas être allumé.
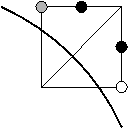
Supposons maintenant que le dernier point allumé est sur la diagonale, c'est-à-dire qu'il est de la forme (x0, x0). On considère alors deux sous-cas.
-
Si le dernier mouvement est vers l'est, alors le point milieu
(x0, x0-1/2) est situé à l'intérieur du cercle (ou sous
l'arc).
On distingue alors encore deux sous-cas.
-
Si (x0,x0) est en dehors du cercle alors le cercle
intersecte le demi-segment unité vertical inférieur centré en
(x0,x0) et ce point doit être allumé.
Il s'agit du cas disgracieux obtenu par exemple pour R=4 et R=11.
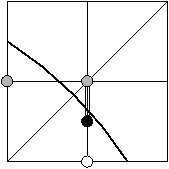
- Sinon,
nous savons par ailleurs que l'arc passe à une distance verticale
inférieure à 1/2 de l'avant dernier point (x0-1,x0).
En appliquant l'interprétation géométrique vers la droite au point
de passage de l'arc par l'axe vertical x=x0-1 on voit que l'arc
coupera l'axe x = x0 sous l'ordonnée x0+1/2.
Ce cas me semble d'ailleurs impossible avec R entier. En effet, x0 est ici la partie entière de 2-1/2 R, on a donc 2 x02 < R2. Par ailleurs, on a (x0-1)2 + (x0+1/2) ≥ R2 et donc x0 ≤ 2 x02 - R2 + 5/4, soit encore x0 < 5/4 et donc x0 = 1. Soit finalement R = 1 ou R = 2 qui ne correspondent pas à la configuration (voir la figure 1). De fait cette configuration survient pour R compris entre 21/2 et 3/2.
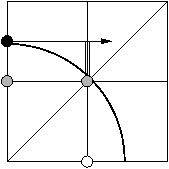
-
Si (x0,x0) est en dehors du cercle alors le cercle
intersecte le demi-segment unité vertical inférieur centré en
(x0,x0) et ce point doit être allumé.
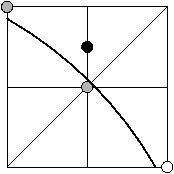
- Si le dernier mouvement est vers le sud-est,
alors le point milieu
(x0, x0+1/2) est situé à l'extérieur du cercle.
-
Si le point (x0,x0) est à l'intérieur, on peut conclure
directement.
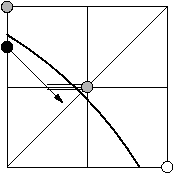
- Sinon, l'arc intersecte nécessairement l'axe x=x0-1 au dessus du
point (x0-1,x0+1/2) et on peut conclure par
l'interprétation géométrique vers la droite à partir de ce point
d'intersection et jusqu'à l'axe y=x0.
-
Si le point (x0,x0) est à l'intérieur, on peut conclure
directement.
Toutefois, il faut éviter la deuxième série de points dans les cas x=0 et x=y.
On notera bien que c'est la conservation de l'approximation de Freeman par toutes ces isométries qui garantit que nous construisons bien une approximation de Freeman du cercle de rayon R centré en (xc, yc).