Arbres

Planche : 1

Diversion

On sait…

Les classes sont les « patrons » (cf. couture) des objets.
Chaque objet possède ses propres composants dynamiques.
Tous les objets partagent les même composants statiques.

Slogan!

Ce qui est static est à la classe, ce qui est dynamique est à l’objet.

class Pair {
  static int count = 0 ;
  int x, y ;

  Pair (int x, int y) {
    this.x = x ; this.y = y ; count++ ;
  }

  public static void main(String [] arg) {
    Pair p = new Pair (1, 2), q = new Pair (2, 3) ;
    System.out.println(count) ;
  }
}

Quelle est la notation « complète » pour count ? Pair.count.
Qu’affiche le programme : 2.

Planche : 3

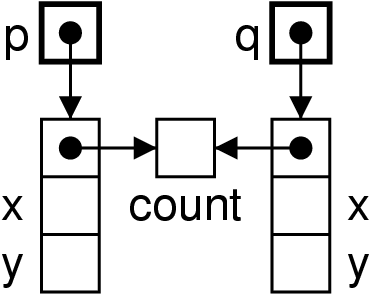
Implémentation (simplification)

Deux objets de la même classe Pair.

Ont chacun leur propres champs x et y.
Pointent vers le vecteur des variables de la classe Pair.

Planche : 4

Cas des méthodes

Le slogan s’applique encore.

Méthode static. Il n’y a même pas besoin de parler d’objet. La méthode existe, c’est tout. Exemple, Integer.parseInt.
Méthode dynamique. Elle est propre à chaque objet. Exemple stack.push(1).
Dans le code d’une méthode dynamique, un objet courant existe, il s’appelle : this.
Dans le code d’une méthode statique on a pas accès aux champs/méthodes dynamiques, car il n’y a pas d’objet.

Planche : 5

Si c’est static, ya pas d’objet

Une petite inattention.

class Pair {
  private int count ;
  int x, y ;
  Pair (int x, int y) {
    this.x = x ; this.y = y ; count++ ;
  }

  static int lireCount() {
    return count ;
  }
}

Est-ce que ça compile ? Non ! Pourquoi ?.

La méthode statique lireCount fait référence à la variable non-statique count.

# javac Pair.java
Pair.java:10: non-static variable count
              cannot be referenced from a static context
    return count ;
           ^

Planche : 6

Quelques exemples de méthodes dynamiques

Codage objet des piles :
Stack s1 = new Stack (), s2 = new Stack () ;
s1.push(1) ; s2.push(2) ;
Sortie standard/d’erreur, System.out/System.err, deux objets différents (rangés dans deux variables de classes…).
System.out.println("Je vais dans out") ;
System.err.println("Je vais dans err") ;
Et si on fait :
```
# java A > bonga
```
- Ça range dans le fichier bonga : « Je vais dans out ».
- Ça affiche : « Je vais dans err ».

Planche : 7

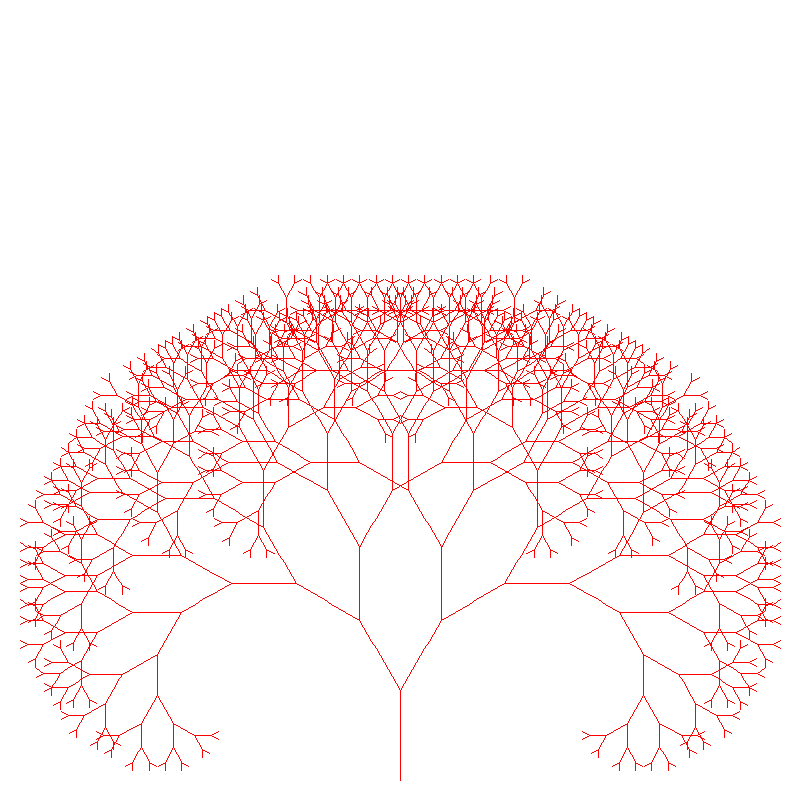
Un arbre dans la nature

Planche : 8

Un arbre dans l’ordinateur

Planche : 9

Structure récursive (« fractale »)

Planche : 10

Au final…

T → D[-T]+T

Planche : 11

Un autre arbre, plus naturel

T → D[-T]D[++T]T

Planche : 12

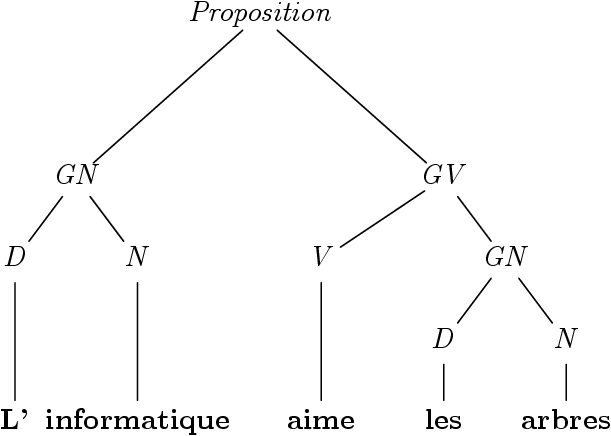
Les arbres « hiéarchie »

Planche : 13

Les arbres structurants

Planche : 14

Ou plus informatiquement…

Planche : 15

Bon et en Java ?

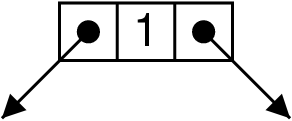
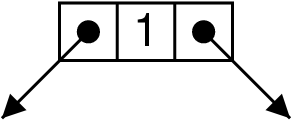
La liste :
L’arbre (binaire) :

Planche : 16

Définition des cellules d’arbre (binaire)

class Tree {
  int val ;
  Tree left, right ;

  Tree (Tree left, int val, Tree right) {
    this.left = left ;
    this.val = val ;
    this.right = right ;
  }
}

Remarquer

Nos arbres ont au plus deux fils.
On retrouve notre dangereux ami, l’arbre vide : null.

Planche : 17

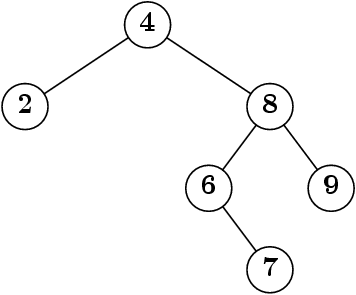
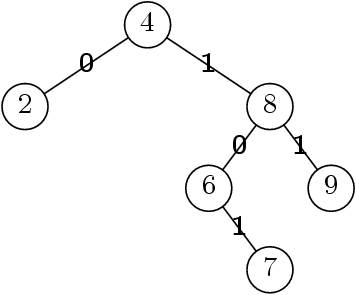
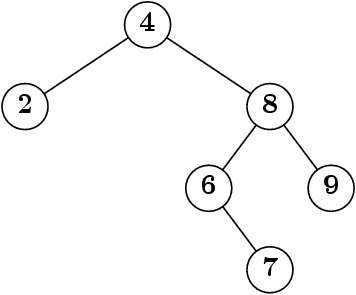
Fabriquons un arbre

new Tree (
   new Tree (null, 2, null),
   4,
   new Tree (
     new Tree (null, 6, new Tree (null, 7, null)),
     8,
     new Tree (null, 9, null)))

Planche : 18

Surcharge du constructeur

Permet de faire un peu plus concis (mais ça n’ira pas loin).

Tree (int val) {
  this.val = val ;
}

new Tree (
   new Tree (2),
   4,
   new Tree  (
     new Tree (null, 6, new Tree (7)),
     8,
     new Tree (9)))

Planche : 19

Arbre et récursivité

Les arbres sont des structures très récursives :

L’arbre vide est un arbre.
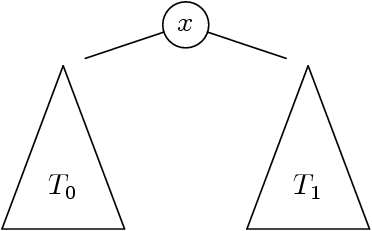
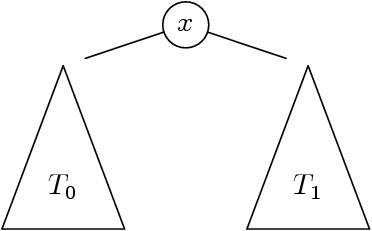
Si T₀ et T₁ sont des arbres, alors (T₀, x, T₁) est un arbre.

On peut voir les arbres comme solutions de cette équation.

T = null ⊎ (T × int × T)

La programmation est systématiquement récursive.

Planche : 20

Vocabulaire

Le « sommet » (ou « nœud ») marqué x est la racine.
Les arbres T₀ et T₁ sont les sous-arbres.
Les racines de T₀ et T₁ sont les fils (enfants) de la racine qui est leur père (parent).
Si T₀ et T₁ sont l’arbre vide, alors le sommet x est une feuille.

En java, arbre ∼ référence, sommet ∼ cellule.

Planche : 21

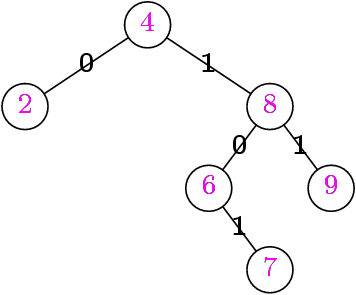
Se repérer dans un arbre

Dans une liste on parlait du k-ième élément, dans un arbre on parle de chemin.

Par exemple le chemin vers la feuille étiquetée 7 est : 1.0.1.

Le chemin vers la racine est : «» (rien ou Λ).

Il est également pratique de repérer les sous-arbres (ex. 0.0).

Bref, les chemins sont tout bêtement des listes.

Planche : 22

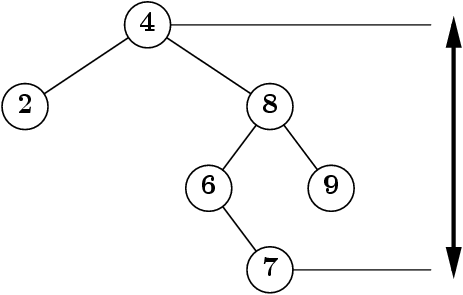
Hauteur

La profondeur d’un sous-arbre est la longueur du chemin qui y mène,

La hauteur d’un arbre est la profondeur maximale de ses sous-arbres
C’est aussi la profondeur maximale des feuilles, plus un (arbres vides).

Planche : 23

Calcul de la hauteur

Il n’y pas le choix : approche… récursive.

H(∅)	=	0
H(T₀, _, T₁)	=	1 + max(H(T₀), H(T₁))

static int getHeight(Tree t) {
  if (t == null) {
    return 0 ;
  } else {
    return 1+Math.max(getHeight(t.left), getHeight(t.right)) ;
  }
}

Planche : 24

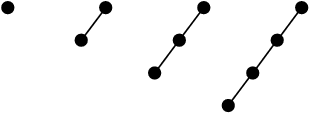
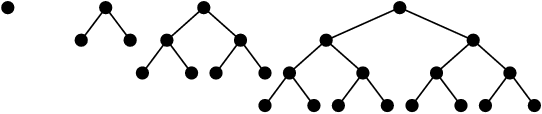
Borner la hauteur

Soit un arbre de hauteur h, contenant n sommets.

h ≤ n ≤ 2^h−1

Arbres avec n minimal :
Arbres avec n maximal :

Soit encore.

log₂(n+1) ≤ h ≤ n

Planche : 25

Trouver un sous-arbre connaissant son chemin

La définition inductive est assez claire :

T/Λ = T, (T₀, _, T₁)/0.C = T₀/C, (T₀, _, T₁)/1.C = T₁/C,

Un Chemin est une liste d’entiers.

static Tree subTree(Tree t, Chemin c) {
  if (c == null) {
    return t ;
  } else if (t == null) {
    throw new Error () ;
  } else if (c.val == 0) {
    return subTree(t.left, c.next) ;
  } else if (c.val == 1) {
    return subTree(t.right, c.next) ;
  } else {
    throw new Error () ;
  }
}

Planche : 26

Trouver son chemin II

Du point de vue du chemin, on effectue un parcours de liste, d’où le code alternatif suivant.

static Tree subTree(Tree t, Chemin c) {
  for ( ; c != null ; c = c.next) {
    // Traiter d'abord l'erreur
    if (t == null) { throw new Error () ; }
    // Ici t n'est pas null
    if (c.val == 0) { t = t.left ; }
    else if (c.val == 1) { t = t.right ; }
    else { throw new Error () ; }
  }
  return t ;
}

De fait, la récursion était terminale (cf. amphi 02).

Planche : 27

Arbres strictement binaires

Les sommets ont zéro ou deux fils. Définition sans l’arbre vide :

Une feuille est un arbre.
Si T₀ et T₁ sont des arbres, alors (T₀, x, T₁) est un arbre.

Attention : en programmation null demeure…(pour repérer les feuilles).

class Tree {
  // Comme avant.

  Tree (int x) { this.val = x; } // Constructeur des feuilles.

  boolean isLeaf() {
    return this.left == null && this.right == null ;
  }
}

Planche : 28

Une amusante propriété des arbres binaires (stricts)

Un arbre binaire strict possède n+1 feuilles et n sommets internes.

n = 0, cas de la feuille (cas de base).
n > 0, soit T = (T₁,T₂) (n₁+1 et n₂+1 feuilles chacun),
- Nombre de feuilles : (n₁ + 1) + (n₂ + 1).
- Nombre de sommets internes : n₁ + n₂ + 1, (ceux de T₁ plus ceux de T₂, plus la racine.

Planche : 29

Parcourir un arbre

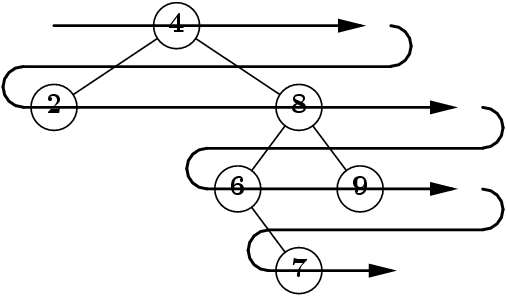
En largeur d’abord.

Si on parcourt pour afficher, on affichera donc :

[4], [2, 8], [6, 9], [7].

C’est conceptuellement assez simple (parcours « par étages » de profondeur croissante), mais un peu délicat à programmer.

Planche : 30

Parcours en profondeur d’abord

Conceptuellement simples, si on veut bien adopter le point de vue récursif :

Parcourir sous-arbres par sous-arbre.
Mais encore :
- Préfixe : x → T₀ → T₁.
- Infixe : T₀ → x → T₁.
- Postfixe : T₀ → T₁ → x.

Il n’y a rien d’autre à comprendre (savoir)!

Planche : 31

Exemple, en profondeur (postfixe)

T₀, T₁, 4.
2, T₁, 4.
2, T₀, T₁, 8, 4.
2, T₀, 9, 8, 4.
2, 7, 6, 9, 8, 4.

Planche : 32

Le plus simple est encore de programmer

Si T est vide, … ne rien faire !
Si T est (T₀, x, T₁), … afficher T₀, T₁ et enfin x.

static void postfix(Tree t) {
  if (t != null) {
    postfix(t.left) ;
    postfix(t.right) ;
    System.out.println(t.val) ;
  }
}

Note : généralisation de l’affichage des listes.

static void print(List p) {
  if (p != null) {
    print(p.next) ; System.out.prinln(t.val) ;
  }
}

Planche : 33

Un problème un peu différent

Calculer la liste des étiquettes (dans l’ordre postfixe).

Solution « théorique »

P(∅)	=	∅
P(T₀, x, T₁)	=	P(T₀) ; P(T₁) ; x

Bon nous voilà bien avancés…

static IntList postfix(Tree t) {
  if (t == null) {
     return null ;
  } else {
    return
      IntList.append(postfix(t.left),
        IntList.append(postfix(t.right),
          new IntList (t.val, null))) ;
  }
}

Planche : 34

Débarassons nous de ces concaténations coûteuses

Généralisons (un peu) le problème. Le mission de P(T, k) est renvoyer la liste des étiquettes de T suivie de la liste k.

P(∅, k)	=	k
P((T₀, x, T₁), k)	=	P(T₀,P(T₁, (x ; k)))

static IntList postfix(Tree t, IntList k) {
  if (t == null) {
    return k ;
  } else {
    return
      postfix(t.left, postfix(t.right, new IntList (t.val,k))) ;
  }
}
static IntList postfix(Tree t) { // Surcharge
  return postfix(t, null) ;
}

Planche : 35

Comment programmer le parcours en largeur

Le point de vue récursif fonctionne mal, pourquoi ?
L’affichage des sous-arbres gauche et droit se mélange !

On va donc avoir recours à un raisonnement plus global.

Il « suffit » en fait d’afficher tous les sommets de profondeur k avant les sommets de profondeur k+1.
Par ailleurs un sommet de profondeur k+1 est toujours fils d’un (unique) sommet de profondeur k.
Donc on peut afficher les sommets de profondeur k et en même temps collecter leurs fils.

Planche : 36

Programmation du parcours en largeur

static void bfs(Tree t) {
  TreeList next = new TreeList(t,null) ; // int k=0 ;
  while (next != null) {  // next -> sous-arbres profondeur k
    TreeList now = next ; // now -> sous-abres profondeur k
    next = null ;
    for ( ; now != null ; now = now.next) {
// pour tous les sous-arbres de profondeur k
      Tree t = now.val ;
      if (t != null) {
        System.out.println(t.val) ; // Afficher
        next = new TreeList (t.left,
                 new TreeList (t.right, next)) ;
        // Collecter les fils (next -> profondeur k+1)
      }
    } // k = k+1 => next -> profondeur k
  }
}

Planche : 37

Programmation traditionnelle de la largeur d’abord

static void bfs(Tree t) {
  Fifo f = new Fifo () ;
  f.enfile() ;
  while (!f.isEmpty()) {
     Tree t = f.defile() ;
     if (t != null) {
       System.out.println(t.val) ;
       f.enfile(t.left) ;
       f.enfile(t.right) ;
     }
  }
}

Pourquoi ça marche ?

Terminaison ? Soit N(T) nombre de sommets et d’arbres vides dans un arbre (nombres de chemins)
Σ_{T ∈ f} N(T) décroit strictement à chaque tour de boucle.

Planche : 38

Exemple de fonctionnement


	Λ

—→

0.1

0.0

—→

1.1

1.0

0.1

0.0

—→…—→

1.1

1.0

—→

1.0.1

1.0.0

1.1

—→

…

Planche : 39

Preuve de correction du parcours avec file

Transitions effectuées sur un état comprenant file F et affichage A.

F=F; (T₀, x, T₁)^k, A=A	⇒	F=T₁^k+1; T₀^k+1; F, A=A; x^k
F=F; ∅^k, A=A	⇒	F=F, A=A

(T à la profondeur k, noté T^k.)

On voit alors que l’on a, en n étapes

F=T₁^k; ⋯; T_n^k, A=A

⇒

F=U₁^k+1; ⋯; U_m^k+1, A=A; x₁^k; ⋯; x_ℓ^k

Ce qui suffit pour montrer, qu’en h grosses étapes, on a :

F=T⁰, A=

⇒

F=, A=A

Où A est une séquence de sommet de profondeurs croissantes.

Planche : 40

Et avec une pile explicite ?

static parcours(Tree t) {
  Stack<Tree> stack = new Stack<Tree> () ;
  stack.push(t) ;
  while (!stack.isEmpty()) {
     Tree t = stack.pop() ;
     if (t != null) {
       System.out.println(t.val) ;
       stack.push(t.right) ;
       stack.push(t.left) ;
     }
  }
}

C’est le parcours : préfixe !

Il est clair que dans (T₀, x, T₁), x est affiché d’abord.
Il est moins clair que T₀ est affiché avant T₁.

Planche : 41

Preuve de l’affichage préfixe avec pile explicite

Transitions effectuées sur un état comprenant pile S et affichage A.

S=S; (T₀, x, T₁), A=A	⇒	S=S; T₁; T₀, A=A; x
S=S; ∅, A=A	⇒	S=S, A=A

Notons P la séquence des sommets dans l’ordre préfixe :

P(∅) =, P(T₀, x, T₁) = x; P(T₀); P(T₁)

On veut montrer

S=S; T, A=A

⇒

S=S, A=A; P(T)

Par induction structurelle sur T (cas de base laissé en exercice).

S=S; (T₀, x, T₁), A=A

⇒

S=S; T₁; T₀, A=A; x

⇒

S=S; T₁, A=A; x;P(T₀)

⇒

S=S, A=A; x;P(T₀); P(T₁)

Planche : 42

Les expressions arithmétiques

⇕
1 + (2 × 3)

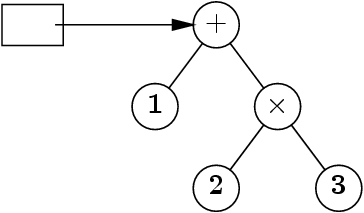
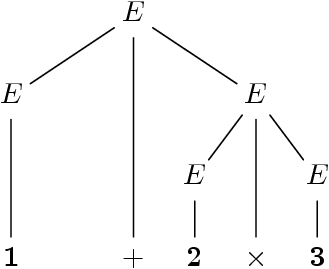
Approche récursive, une expression est :

Un entier (une feuille x).
Une « opération » (E₁, ⊕, E₂) (un sous-arbre binaire).

Inportant : Il n’y a pas d’arbre vide.

Planche : 43

Réalisation simple

class Exp {
  final static int OP=0, INT=1 ;
  int nature ; // champ 'indicateur'

  int val ;   // valide si nature == INT
  char op ; Exp left, right ; // valides si nature == OP

  Exp (int val) {
    nature = INT ; this.val = val ;
  }

  Exp (Exp left, char op, Exp right) {
    nature = OP ;
    this.op = op ; this.left = left ; this.right = right ;
  }
}

Planche : 44

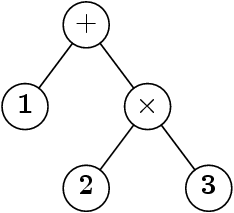
Construction, avec les constructeurs

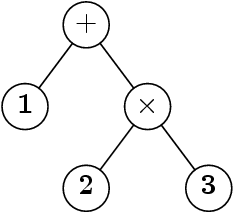
  Exp e = new Exp(
      new Exp(1),
      '+',
      new Exp (new Exp(2), '*', new Exp(3))) ;

C’est lourd et en fait assez eloigné des habitudes.

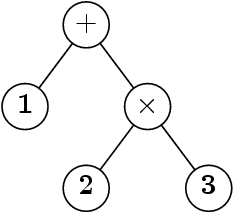
Habituellement, on écrit 1 + 2 × 3 et on « comprend » l’arbre.

Planche : 45

Pour le moment

Transformer les expressions écrites linéairement (notation infixe) en arbre est trop compliqué (cf. INF 431).
Mais nous saurons le faire avec des opérations en notation postfixe ! Avec une pile (d’expressions).
- Un entier x : empiler la feuille new Exp(x).
- Un opérateur ⊕ : dépiler x, dépiler y, empiler,new Exp (y, ⊕, x).
C’est très similaire à la calculette d’il y a quinze jours.

Planche : 46

Exemple d’exécution du lecteur d’expressions

—→¹

—→²

—→³

—→^×

—→⁺

Planche : 47

Réalisation du lecteur d’expressions

class Exp {
  public static void main (String [] arg) {
    Stack<Exp> stack = new Stack<Exp> ;
    for (int i = 0 ; i < arg.length ; i++) {
      String cmd = arg[i] ;
      if (cmd.equals("+")) {
        Exp x = stack.pop(), Exp = stack.pop() ;
        stack.push(new Exp (y, '+', x));
      } else if …
      // Idem pour "*", "/", "-"
      } else {
        stack.push(new Exp (Integer.parseInt(cmd))) ;
      }
    }
    Exp t = stack.pop() ;
  }
}

Planche : 48

Que faire de nos arbres ?

Les évaluer,
static int eval(Exp e) {
  if (e.nature == INT) {
    return e.val ;
  } else if (e.nature == OP) {
    switch (e.op) {
      case '+': return eval(e.left) + eval(e.right)  ;
      case '-': return eval(e.left) - eval(e.right)  ;
      case '*': return eval(e.left) * eval(e.right)  ;
      case '/': return eval(e.left) / eval(e.right)  ;
     }
  }
  throw new Error ("eval") ;
}
Les afficher (sous forme infixe!).
Les dériver…

Planche : 49

Résumons nous

Il y a beaucoup de points de vue sur les arbres.

Le point de vue pointeur :
Le point de vue récursif :
T = null ⊎ (T × int × T)
Le point de vue cas particulier des graphes (cf. poly).
Un arbre est un graphe non orienté, non vide, connexe et sans circuit. Un sommet distingué est la racine.
Autrement dit, si on le dessine, on a un arbre !

Planche : 50

Les arbres n-aires

Un sommet possède un nombre arbitraire de fils.

L’arbre vide est un arbre.
Si L est une liste d’arbre, alors (x,L) est un arbre.

Les diverses notions (parcours, etc.) restent naturelles.

En Java :

class Tree {
  int val ;
  TreeList sons ;
  Tree (int val, TreeList sons) {
    this.val = val ; this.sons = sons ;
  }
}

class TreeList { … }

Planche : 51

Soyons souples

Selon les circonstances, les listes peuvent être remplacées par des tableaux, des tableaux extensibles (ArrayList<Tree>) etc.

import java.util.* ;
class Tree {
  int val ;
  ArrayList<Tree> sons ;

  Tree (int val, ArrayList<Tree> sons) {
    this.val = val ; this.sons = sons ;
  }

  Tree (int val, Tree t1, Tree t2) {
    this.val = val ;
    this.sons = new  ArrayList<Tree> () ;
    this.sons.add(t1) ; this.sons.add(t2) ;
  }
}

Planche : 52

Un petit exercice

Pour bien se convaincre que les arbres, c’est récursif : calculer tous les chemins !

C(∅)	=	Λ ; ∅
C(T₀, _, T₁)	=	Λ ; { 0.u ∣ u ∈ C(T₀) } ; { 1.u ∣ u ∈ C(T₁) }

Clairement, on a besoin d’une fonction auxiliaire : (qui réalise { X.u ∣ u ∈ U }).

Cette fonction prend en argument un entier (0 ou 1) et une liste de chemins et renvoie : une liste de chemins.

A(x, ∅)	=	∅
A(x, u ; U)	=	(x; u) ; A(x, U)

Planche : 53

La fonction A

Chemin sont des listes d’entiers et Chemins des listes de listes d’entiers comme d’habitude.

static Chemins add (int x, Chemins us) {
  if (us == null) {
    return null ;
  } else {
    return
     new Chemins
       (new Chemin (x, us.val),
        add (x, us.next)) ;
  }
}

Planche : 54

Tous les chemins

C(∅)	=	Λ ; ∅
C(T₀, _, T₁)	=	Λ ; A(0, C(T₀)) ; A(1, C(T₁))}

static Chemins getPaths (Tree a) {
  if (a == null) {
    return new Chemins (null, null) ;
  } else {
    Chemins pathsLeft = getPaths(a.left) ;
    Chemins pathsRight = getPaths(a.right) ;
    return
      new Chemins
        (null,
        Chemins.append
          (add(0, pathsLeft), add(1, pathsRight))) ;
  }
}

Planche : 55

Éviter les concaténations

static Chemins add (int x, Chemins us, Chemins k) {
  if (us == null) {
    return k ;
  } else {
    return
     new Chemins
       (new Chemin (x, us.val),
        add (x, us.next, k)) ;
  }
}

Planche : 56

Tous les chemins

static Chemins getPaths (Tree a) {
  if (a == null) {
    return new Chemins (null, null) ;
  } else {
    Chemins pathsLeft = getPaths(a.left) ;
    Chemins pathsRight = getPaths(a.right) ;
    return
      new Chemins
        (null, add(0, pathsLeft, add(1, pathsRight, null))) ;
  }
}

Ce document a été traduit de L^AT_EX par H^EV^EA