Un peu de listes Piles, Files

Planche : 1

Détour : les sacs

Les piles et les files sont des cas particuliers des sacs.

Les opérations suivantes sont définies sur les sacs

Le sac est-il vide ?
Ranger dans le sac,
Sortir un élément du sac (un des éléments rangés au préalable).

Le sac typique (en style objet) :

class Bag {
  …
  Bag () { … }
  boolean isEmpty() { … }
  void put(Object o) { … }
  Object get() { … }
}

Remarquer : Le sac est une structure mutable.

Planche : 2

Les piles et les files

Piles et files sont des sacs munis de règles supplémentaires reliant les sorties et les entrées :

Les piles sont des sacs « évangéliques » : dernier entré, premier sorti (ou LIFO : Last In, First Out).
- En ce cas, put se dit souvent push (empiler) et get se dit souvent pop (dépiler).
Les files sont des sacs égalitaires : premier entré, premier sorti (ou FIFO : First In, First Out).
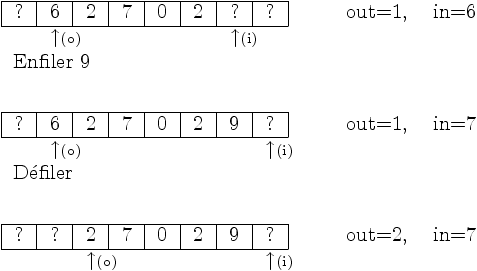
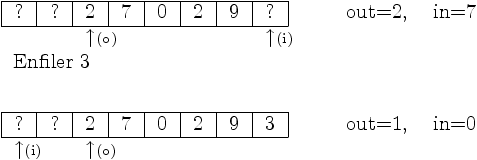
- En ce cas, put peut se dire enfiler et get peut se dire défiler.

Planche : 7

À quoi ça sert ?

La file est la structure la plus intuitive.

La file sert par exemple, dans un système d’exploitation, à servir des demandes d’impression dans l’ordre.

Il y a une file spool des fichiers à imprimer.
Chaque utilisateur demande l’impression d’un fichier f par :
…spool.put(f)…
Tandis qu’un acteur quelconque du système d’exploitation exécute (conceptuellement) la boucle suivante :
   for ( ; ; ) { // Boucle infinie, comme « while (true) { »
     if (!spool.isEmpty()) {
       Fichier f = spool.get() ;
       … // Réellement envoyer f à l'imprimante.
     }
   }

Planche : 8

À quoi ça sert ?

La pile est la structure la plus « informatique ».

Son besoin se fait clairement sentir dans la situation suivante…

Un cuisinier fait une sauce…
- Chef, votre épouse au téléphone ! Mettre la sauce en attente (empiler(sauce)) et répondre…
  - Chef, il y a le feu ! Mettre le téléphone en attente (empiler(téléphone)) et aller éteindre le feu.
  - Le feu est éteint…
- Dépiler la tâche en attente (téléphone) et la terminer…
Dépiler la tâche en attente (sauce) et la terminer.

Planche : 9

Autre utilisation des piles

Évaluation des expressions arithmétiques.

Soit les piles d’entiers :

class Stack {
  …
  Stack () { … }
  boolean isEmpty() { … }
  void push(int i) { … }
  int pop() { … }
}

Les calculettes en notation postfixe (ou « polonaise ») fonctionnent à l’aide d’une pile, selon ce principe :

Un entier → l’empiler.
Une opération ⊕, depiler x, dépiler y, empiler ⊕(y, x).

Planche : 10

Exemples de calcul en notation postfixe

Calculer 1 + (2 × 3) : 1 2 3 * + (ou 2 3 * 1 + d’ailleurs).

→ 1 →

→ 2 →

→ 3 →

→ × →

→ + →

Calculer (1 + 2) × 3 : 1 2 + 3 *

→ 1 →

→ 2 →

→ + →

→ 3 →

→ × →

class Calc {
  public static void main (String [] arg) {
    Stack stack = new Stack () ;
    for (int i = 0 ; i < arg.length ; i++) {
      String cmd = arg[i] ;
      if (cmd.equals("+")) {
        int x = stack.pop(), y = stack.pop() ;
        stack.push(y+x) ;
      } else if …
      // Idem pour "*", "/", "-"
      } else {
        stack.push(Integer.parseInt(cmd)) ; // doc
      }
    }
    System.out.println(stack.pop()) ;
  }
}

Planche : 12

Exécution de Calc

% java Calc 1 2 + 3 '*'
1 -> [1]
2 -> [1, 2]
+ -> [3]
3 -> [3, 3]
* -> [9]
9

Mais…

% java Calc 1 +        
1 -> [1]
Exception in thread "main" java.util.EmptyStackException
        at java.util.Stack.peek(Stack.java:79)
        at java.util.Stack.pop(Stack.java:61)
        at Calc.main(Calc.java:9)

Planche : 13

Précisions sur la notation postfixe

Par définition, une notation postfixe est une suite de symboles P.

P	=	int
	∣	P₁ P₂ op

Par exemple :


0
◥	▼	◤


1 2 +
◥	▼	◤


3
◥	▼	◤

◥

▼

◤

◥

▼

◤

Par définition, la valeur d’une notation postfixe est :

v(int)	=	int
v(P₁ P₂ op)	=	op(v(P₁), v(P₂))

Planche : 14

Correction du calcul

Modélisons le programme Calc. Son état : ⟨ I • S ⟩.

L’entrée I, c’est-à-dire une suite de symboles.
La pile S (d’entiers).

Une action consiste à lire le symbole.

⟨
⟨

int I • S

⟩
⟩

→

⟨
⟨

I • S, int

⟩
⟩

⟨
⟨

op I • S, v₁, v₂

⟩
⟩

→

⟨
⟨

I • S, op(v₁, v₂)

⟩
⟩

Théorème Si I est une notation postfixe P, alors la pile S contient v(P) à la fin.

⟨
⟨

P •

⟩
⟩

→^*

⟨
⟨

• v(P)

⟩
⟩

Planche : 15

Lemme Pour toute suite de symboles I, toute pile S, et toute notation postfixe :

⟨
⟨

P I • S

⟩
⟩

→^*

⟨
⟨

I • S, v(P)

⟩
⟩

Démonstration Par induction (sur P). Dans le cas P = P₁ P₂ op.

⟨
⟨

P I • S

⟩
⟩

⟨
⟨

P₁ P₂ op I • S

⟩
⟩

→^*

⟨
⟨

P₂ op I • S , v(P₁)

⟩
⟩

→^*

⟨
⟨

op I • S , v(P₁) , v(P₂)

⟩
⟩

→

⟨
⟨

I • S , op(v(P₁), v(P₂))

⟩
⟩

⟨
⟨

I • S , v(P)

⟩
⟩

Planche : 16

Pile et appel de méthode

Revenons sur la fusion récursive qui échoue par « débordement de la pile » pour des listes assez longues.

static List merge(List xs, List ys) {
  if (xs == null) {
    return ys ;
  } else if (ys == null) {
    return xs ;
  } // NB: désormais xs != null && ys != null
    else if (xs.val <= ys.val) {
    return new List (xs.val, merge(xs.next, ys)) ;
  } else { // NB: ys.val < xs.val
    return new List (ys.val, merge(xs, ys.next)) ;
  }
}

Planche : 17

Appel de méthode

En simplifiant un peu.

Le système d’exécution Java dispose d’une pile.
Pour appeler une méthode :
- Empiler une addresse de retour.
- Empiler les arguments de la méthode.
Une méthode
- Prélude : récupérer les arguments.
- Code de la méthode proprement dit… qui rend la pile dans l’état où il l’a trouvée.
- Postlude : (pour revenir)
  - Dépiler l’adresse de retour.
  - Empiler le résultat de la méthode.
  - Transférer le contrôle du programme à l’adresse de retour.

Planche : 18

Dans le cas qui nous occupe

Nous allons modéliser un processeur en Java, et examiner ce que fait le code compilé de merge.

Toutes les variables sont globales (registres).
Le contrôle est explicite (code = séquence d’instructions).
- Il y a des étiquettes (points dans l’exécution).
- Il y a des instructions « goto » (transfert direct) et « goto* » (transfert indirect).

merge: // « Étiquette » de début de la méthode.
/* La pile S est P , ret , xs , ys
   Il faut rendre P , merge(xs, ys) */
  ys = S.pop() ;
  xs = S.pop() ;
  if (xs == null) {
    lab = S.pop() ; S.push(ys) ; goto* lab ;
  } …

Planche : 19

Appel récursif

  ⋮
/* La pile S est P , ret
   Il faut rendre P , merge(xs, ys) */
  if (xs.val <= ys.val) {
     S.push(xs.val) ; // Sauver xs.val dans la pile
     S.push(lab1) ; S.push(xs.next) ; S.push(ys) ;
     // S est P , xs.val , lab1 , xs.next , ys
     goto merge ; // Appel récursif
   lab1:
     // S est P , merge(xs.next, ys)
     r = S.pop() ;          // Résultat de l'appel
     xsPointVal = S.pop() ; // xs.val sauvé avant l'appel
     lab = S.pop() ;        // Étiquette de retour
     S.push(new List (xsPointVal, r)) ;
     goto* lab ; // La pile est P , merge(xs, ys) ok.
  } …

Planche : 20

Codage des piles (d’entiers)

Le principe est le suivant :

L’objet pile (classe Stack) maintient une liste (privée) d’entiers.
Opérations :
- Ajouter au début de la liste,
- Enlever du début de la liste.

class Stack {
  private List me ;
  Stack () { me = null ;  }
  boolean isEmpty() { return me == null ; }
  …
}

Planche : 21

Diversion : modificateurs de visibilité

Le champ me des objets Stack est déclaré private.

class Stack {
private List me ; …

En effet, il ne faut pas que qui que ce soit d’autre (que l’objet Stack) utilise me.

Les modificateurs, du plus restrictif au plus permissif.

private, visible de la classe uniquement.
rien, visible du package (un paquet de classes).
protected visible des héritiers (une nouvelle notion).
public visible de partout.

Puisque nous n’utilisons ni package, ni héritage, on se limite à private et à rien. (sauf pour public static void main).

Planche : 22

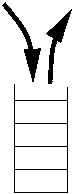
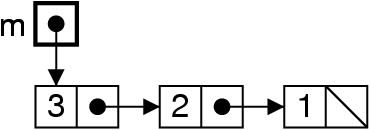
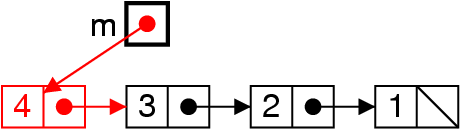
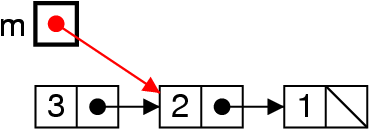
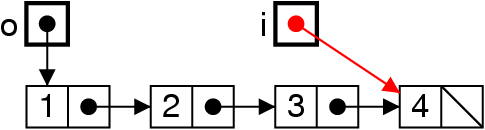
Empiler : ajouter au début

me = new List (4, me) ;

Planche : 23

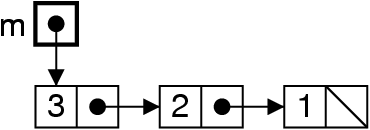
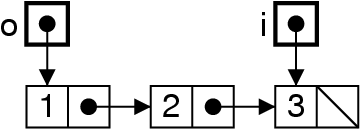
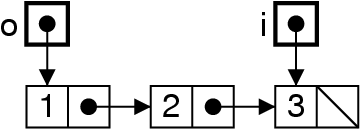
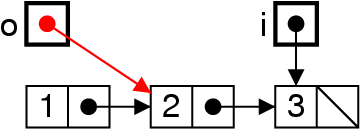
Dépiler : enlever du début

me = me.next ;

Planche : 24

Code de push et pop

  void push(int i) {
    me = new List (i, me) ;
  }

  int pop() {
    if (me == null) throw new Error("Pile Vide") ;
    int r = me.val ;
    me = me.next ;
    return r ;
  }

Remarquer « throw new Error(…) » qui interrompt le programme en lançant (instruction throw) une exception (ici objet de la classe Error).

Planche : 25

Diversion : programmation des erreurs

Si l’effet attendu d’une erreur est de faire échouer le programme, on se demande bien l’intérêt de l’exception.

System.err.println("Erreur : pile vide") ; // NB sortie d'erreur
System.exit(2) ; // Tout arrêter

Mais on veut pouvoir réparer les erreurs dans le programme.

Or, une exception est un résultat innattendu, qui passe par tous les appels en attente.

% java Calc 1 +        
1 -> [1]
Exception in thread "main" java.util.EmptyStackException
        at java.util.Stack.peek(Stack.java:79)
        at java.util.Stack.pop(Stack.java:61)
        at Calc.main(Calc.java:9)

Et on peut « attraper » l’erreur au passage.

Planche : 26

Signaler une erreur

Déclarer une classe de nos exceptions (plus propre).

class StackEmpty { } extends Exception

Lancer notre exception.

int pop() throws StackEmpty { // Obligatoire ici
if (me == null) throw new StackEmpty () ;
…

Note : Le code la classe Stack se contente de signaler l’erreur.

Cette classe n’est pas modifiable (par ex. code de la bibliothèque).

Planche : 27

Traiter l’erreur

Comme la vraie calculette HP: une pile « vide » contient en fait 0, 0, …

Attraper l’exception (∼ résultat exceptionnel) pour la rempacer par un résultat normal.

static int popStack(Stack s) {
  try {
    return s.pop() ;
  } catch (StackEmpty e) {
    return 0 ;
  }
}

Et appeler popStack(s) en place de s.pop(). dans Calc.

Planche : 28

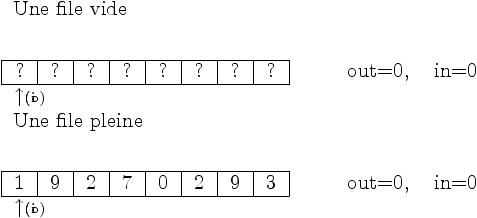
Réalisation des files

Le principe est le suivant, l’objet file maintient une liste (privée) d’entiers.

Ajouter à la fin,
Enlever du début.

Pour réaliser ces opérations en temps constant il nous faut deux références :

in sur la dernière cellule de liste (pour ajouter).
out sur la première cellule de liste (pour enlever).

class Fifo {
  private List in, out ;
  Fifo () { in = out = null ; }
  boolean isEmpty() { return in == null && out == null ; }
  …
}

Planche : 29

Enfiler : ajouter à la fin

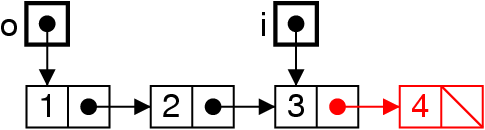
in.next = new List (4, null) ;

Planche : 30

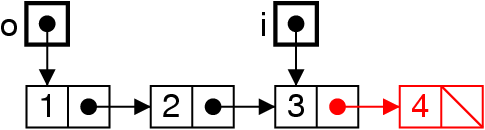
Enfiler : ajouter à la fin (suite)

i = i.next ;

Planche : 31

Défiler : enlever du début

out = out.next ;

Planche : 32

Code complet d’enfiler

Le code final doit tenir compte des files vides.

void enfiler(int i) {
   if (isEmpty()) {
     in = out = new List (i, null) ;
   } else {
     in.next = new List (i, null) ;
     in = in.next ;
   }
}

Il en va de même pour défiler (attention à bien remettre in à null en cas de défilage du dernier élément.)

Planche : 33

Autre réalisation des piles/files

Pile et files peuvent également être codées à l’aide de tableaux.

Voici l’exemple des piles :

class Stack {
  private final static int SZ=32 ; // Taille de pile
  private int [] t ;
  private int sp ; // « pointeur de pile »
  Stack() { t = new int[SZ] ; sp = 0 ; }
  …
}

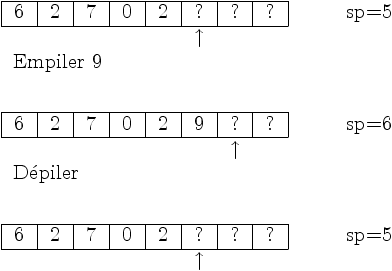
Principe : le tableau est rempli de 0 à sp-1.

pop : sp = sp-1 ;
push(x) : t[sp] = x ; sp = sp+1 ;

Planche : 34

La pile avec un tableau

class Stack {
  …
  boolean isEmpty() { return sp <= 0 ; } // Expression booléenne

  int pop() {
    if (isEmpty()) throw new Error ("Pile vide") ;
    return t[--sp] ; // pour sp = sp-1 ; return t[sp] ;
  }

  void push(int x) {
    if (sp >= t.length) {
      throw new Error ("Pile pleine") ; // Comme Java!
    }
    t[sp++] = x ; // Pour t[sp] = x ; sp = sp+1 ;
  }
}

Planche : 35

Exemple de pile tableau

Planche : 36

Redimensionnement automatique

Il est dommage de limiter la taille des piles à priori.

Profitons des tableaux « dynamiques » de Java.

// Double la taille du tableau interne
  private void resize() {
    if (sp >= t.length) {
      int [] newT = new int [2*t.length] ; // Allouer
      for (int i = 0 ; i < sp ; i++) {
        newT[i] = t[i] ;
      } // Copier t[0..sp] -> newT[0..sp]
      t = newT ; // t référence vers nouveau tableau
    }
  }

  void push(int x) {
    resize() ; t[sp++] = x ;
  }

Planche : 37

Coût de push en cas de redimensionnement

Jusqu’ici push et pop s’exécutaient en temps constant.

Ce n’est plus le cas : push peut maintenant prendre un temps arbitrairement long.

Mais push est toujours en O(1) « amorti ».

Un programme fait N fois push.
Le tableau est initialement de taille 2^p₀.
Au pire le tableau est redimensionné p+1−p₀ fois (2^p < N ≤ 2^p+1). Pour un coût total de l’ordre de :
2^p₀ + 2^p₀+1 + ⋯ + 2^p+1 < 2^p+2 < 4 · N
Le coût de N push est en O(N).
Le coût amorti d’un push est en O(1) (coût total/nb push < cst).

Planche : 38

Les piles toutes faites

La pile est une structure tellement utile, que la bibliothèque Java la propose, classe Stack, package java.util

Mais des piles de quoi ?

La classe Stack est une classe « générique » qui prend une classe en argument.
Les objets de la classe Stack<C> sont des piles de C, où C est une classe arbitraire.

Par exemple Stack<String>, Stack<List>, …

Voir la doc

Planche : 39

Exemple, pile de String

Notation postfixe → Notation infixe (usuelle).

import java.util.* ; // Stack est java.util.Stack
class Infix {
  public static void main (String [] arg) {
    Stack<String> stack = new Stack<String> () ;
    for (int k = 0 ; k < arg.length ; k++) {
      String x = arg[k] ;
      if (x.equals("+") || …) {
        String i1 = stack.pop(), i2 = stack.pop() ;
        stack.push("(" + i2 + x + i1 + ")") ;
      } else {
        stack.push(x) ;
      }
      System.err.println(x + " -> " + stack) ;
    }
    System.out.println(stack.pop()) ;
  }}

Planche : 40

Exemple de transformation

% java Infix 1 2 + 3 '*'
1 -> [1]
2 -> [1, 2]
+ -> [(1+2)]
3 -> [(1+2), 3]
* -> [((1+2)*3)]
((1+2)*3)

Planche : 41

Piles de scalaires

Dans Stack<C> C est une classe.

On ne peut pas faire des piles Stack<int>.

Mais on peut faire des piles Stack<Integer>, où Integer est une classe fournie par défaut (package java.lang).

Deux méthodes utiles :

public static Integer valueOf(int i), du scalaire vers l’objet.
public int intValue(), et réciproquement.

Il y a des classes semblables (Char, Short etc.) pour tous les types scalaires (char, short etc.)

Planche : 42

La calculette avec pile de la bibliothèque

Cela semble assez lourd.

import java.util.* ;
class Calc {
  public static void main (String [] arg) {
    Stack<Integer> stack = new Stack<Integer> () ;
    …
        int i1 = stack.pop().intValue() ;
        int i2 = stack.pop().intValue() ;
        stack.push(Integer.valueOf(i2+i1)) ;
    …
  }
}

Planche : 43

La calculette avec pile de la bibliothèque II

Mais en fait le compilateur sait faire les conversions int ↔ Integer tout seul.

import java.util.* ;
class Calc {
  public static void main (String [] arg) {
    Stack<Integer> stack = new Stack<Integer> () ;
    …
        int i1 = stack.pop(), i2 = stack.pop() ;
        stack.push(i2+i1) ;
    …
  }
}

Attention, le code qui s’exécute est bien par exemple stack.push(Integer.valueOf(i2+i1)).

Planche : 44

Une file dans un tableau, principe

Deux champs privés, int in et int out. La file va de la case out à la case in-1.

Planche : 45

File dans le tableau, difficulté I

Le tableau est « circulaire »

Solution, incrémenter modulo la taille du tableau.

Planche : 46

File dans le tableau, difficulté II

in et out ne suffisent pas toujours.

Solution, conserver une information additionelle : le nombre d’éléments de la file.

Planche : 47

Files de la bibliothèque

Une classe commode LinkedList<C> (package java.util) convient, il s’agit en fait d’une double-ended queue.

La documentation de la classe LinkedList<C>.

Méthodes addFirst et addLast (put) pour ajouter un élément au debut ou à la fin.
Méthodes removeFirst (get) et removeLast pour récupérer le premier ou dernier élément.
Le tout en temps constant, par des listes doublement chaînées (voir le poly, section 2.3.3)

D’autres classes de bibliothèque existent avec des noms plus séduisants (Queue), mais LinkedList<C> est la plus commode.

Planche : 48

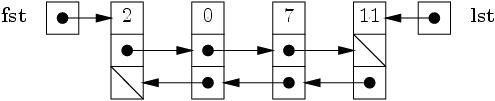
Queue à deux bouts

Un petit exemple,

Par les liens → on a facilement removeFirst/addLast — comme une file, en fait.
Par les liens ← on a facilement removeLast/addFirst — par symétrie, file du dernier au premier élément.

Planche : 49

Choix de l’implémentation

Hors considérations de facilité ou d’efficacité, il n’y a pas à choisir : le service rendu est le même (type abstrait de données).
Si on veut examiner la question…
- Bibliothèque, aucun code à écrire, mais il faut lire la doc, et la comprendre.
- Listes, grande souplesse.
- Tableaux (redimensionné), à priori plus efficace, mais attention à l’occupation mémoire.

Planche : 50

Une autre utilisation des files/piles

Soit un petit robot, perdu dans un labyrinthe, mais muni d’un sac (de cases) d’un pinceau et de trois couleurs. Le robot cherche la sortie ainsi :

  bag.put(entrée) ;
  while (!bag.isEmpty()) {
    Case case = bag.get() ;
    case.colorie(rouge) ;
    if (case.equals.(sortie)) return ;
    for ( … ) { // Tous les voisins non-coloriés
      Case voisin = … ;
      voisin.colorie(bleu) ;
      bag.put(voisin) ;
    }
    case.colorie(vert) ;
  }

Planche : 51

Rapport voisins/couleur

La case rouge vient de sortir du sac,
elle est nécessairement voisine d’au moins une case verte,
la case noire indique un mur.

⇒

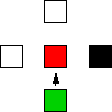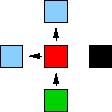Les deux cases voisines accessibles et non encore coloriées entrent dans le sac (en bleu).

Planche : 52

Mettre les voisins dans le sac (file ici)

⇒

Planche : 53

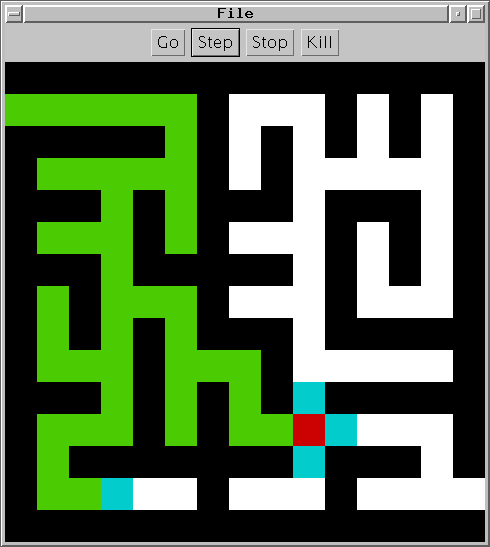Sortir une case de la file

⇒

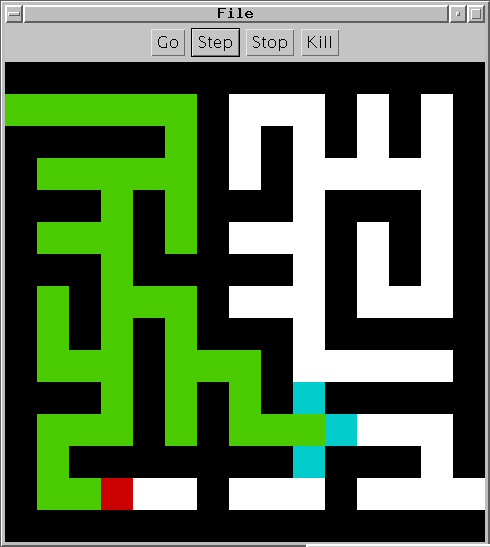Noter : c’est la case la plus ancienne qui est sortie de la file.

Planche : 54

Différents sacs, différents parcours

Sur un labyrinthe sans murs, l’effet est notable.



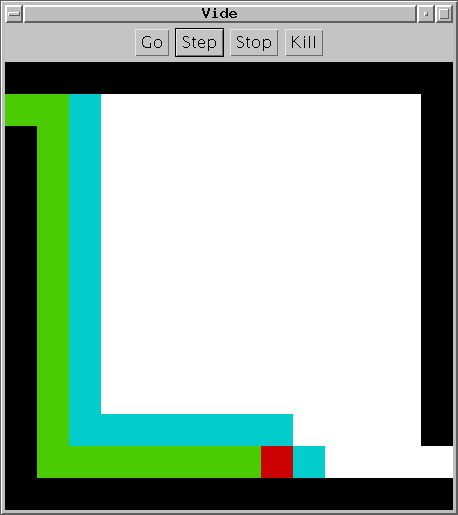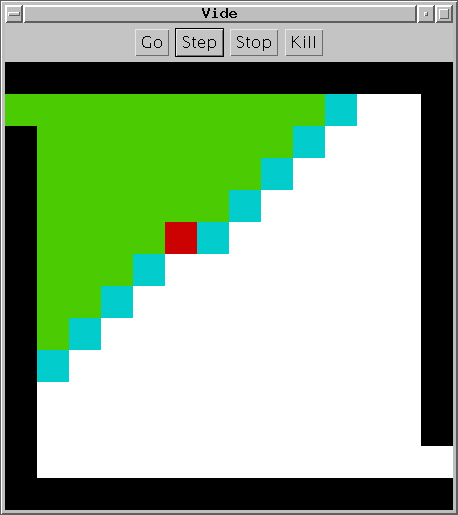Pile		File

Ce document a été traduit de L^AT_EX par H^EV^EA