Votre opinion sur le cours de ce matin :	Votre opinion sur le TD de la semaine dernière :

On rappelle qu'une file est une structure de données dans laquelle on peut mettre des éléments et en prendre, de sorte que les éléments pris le sont dans l'ordre dans lequel ils ont été mis (premier entré premier sorti). On rappelle aussi qu'un tas est un arbre dans lequel les clefs croissent le long des branches, c'est-à-dire que la clef d'un nœud est toujours inférieure ou égale à la clef de chacun de ses fils. Ici, une clef est un entier, qui représente une priorité.

L'objectif de ce TD est d'implémenter les tas binomiaux qui sont une structure particulière permettant de programmer efficacement des files de priorité. Celles-ci sont une variante des files dans lesquelles les éléments sont entrés avec une priorité (qui est un entier) et sortent par ordre de priorité : les éléments de plus petite priorité sortent en premier, et dans le cas où la file contient plusieurs éléments de priorité minimale, l'élément entré en premier sort en premier.

Le TD devra être réalisé en OCaml. On pourra utiliser soit utiliser Eclipse, soit un éditeur de texte classique (par exemple Emacs).

Arbres binomiaux

Nous allons commencer par définir un module BinomialTree permettant de définir des tas fondés sur des arbres particuliers, appelés arbres binomiaux. Dans ces arbres un nœud peut avoir un nombre quelconque de fils, et l'ordre des fils importe.

• Définir un type 'a tree d'arbre dont les nœuds sont étiquetés par une priorité qui est un entier, et une valeur de type quelconque 'a. Un nœud peut avoir un nombre quelconque de fils. La structure de données devra être immuable (on ne modifiera pas la priorité ou la valeur d'un nœud).
• Définir une fonction node : int -> 'a -> 'a tree qui prend en argument une priorité et une valeur et renvoie un arbre à un nœud.

L'ensemble des arbres binomiaux de rang k est défini inductivement par :

• un arbre réduit à une feuille est un arbre binomial de rang 0,
• étant donnés deux arbres binomiaux T et U de rang k, on obtient un arbre binomial de rang k+1, en ajoutant U comme fils le plus à gauche de la racine de T.

                                   

• Écrire une fonction link qui prend deux arbres binomiaux de même rang k et crée un nouvel arbre binomial de rang k+1 selon la méthode précédente.
• Montrer qu'un arbre binomial de rang k a toujours 2^k nœuds.
• À titre d'exercice (cela ne sera pas utilisé par la suite), écrire une fonction size qui calcule le nombre de nœuds d'un arbre. Il pourra être utile de simultanément définir une fonction auxiliaire size_list qui calcule la somme des tailles d'une liste d'arbres en utilisant la structure de code suivante :

  let rec size t =
    ...
  and size_list = function
    | []     -> ...
    | t :: l -> ...
  

  Vérifier la propriété précédente sur quelques exemples :

  let () =
    let zero = node 0 "a" in
    let one = link zero zero in
    let two = link one one in
    assert (size two = 4)
          

• Écrire une fonction rank qui calcule le rang d'un arbre et la tester :

  let () =
    let zero = node 0 "a" in
    let one = link zero zero in
    let two = link one one in
    assert (rank two = 2)
          

• Écrire une interface BinomialTree.mli pour ce module. Le type 'a tree devra être abstrait (on veut pouvoir modifier son implémentation par la suite) et déclarer les fonctions ci-dessus (node, link et rank).
• Modifier la fonction link de sorte à lever une exception lorsque les deux arbres donnés en argument n'ont pas le même rang (c'est le seul cas dans lequel la fonction a du sens).
• La fonction rank étant maintenant couramment utilisée, on souhaiterait qu'elle soit effectuée le plus efficacement possible. Modifier la structure d'arbre 'a tree afin de maintenir le rang et modifier l'implémentation de rank pour qu'elle soit calculée en temps constant. On s'efforcera de conserver la même interface (mli) : la déclaration de 'a tree comme type abstrait a permis d'améliorer l'implémentation sans changer la signature du module.
• Modifier la fonction link de sorte que si ses arguments sont des tas (i.e. la priorité d'un nœud est toujours plus petite que celle de l'un de ses fils), le résultat soit encore un tas, quitte à échanger le rôle des deux arguments.

Déposer les fichier BinomialTree.ml et BinomialTree.mli :

Addition d'entiers binaires

Afin de s'exercer pour la partie suivante, nous allons implémenter dans un autre module Binary quelques manipulations simples d'entiers binaires codés comme des listes d'entiers : un entier binaire sera codé par la liste croissante des indices des bits à 1 dans son écriture binaire. Par exemple, l'entier 19, dont l'écriture binaire est 10011, sera codé par la liste [0;1;4]. On notera binary = int list le type des entiers binaires codés de cette façon. Le module aura l'interface Binary.mli suivante :

type binary

val to_int : binary -> int

val of_int : int -> binary

val add_bit : binary -> int -> binary

val add : binary -> binary -> binary
      

type binary = int list

let to_int b =
  (* à compléter *)
  assert false

let of_int n =
  (* à compléter *)
  assert false

let add_bit b k =
  (* à compléter *)
  assert false

let add b1 b2 =
  (* à compléter *)
  assert false
      

• Coder des fonctions de conversion to_int : binary -> int et of_int : int -> binary et testez-les :

  let () =
    assert (to_int [0;1;4] = 19);
    assert (of_int 19 = [0;1;4])
          

  On peut calculer 2^k via l'expression 1 lsl k (lsl signifie logical shift left). On peut obtenir le dernier bit d'un entier positif n en calculant n mod 2 (qui vaudra 0 ou 1). On peut « effacer » le dernier bit d'un entier n en calculant n/2. Indice: vous pourrez écrire une fonction auxiliaire of_int_aux, de type int -> int -> binary, telle que of_int_aux convertit l'entier 2^kn en une liste. Intuitivement, l'entier n est un entier dont on a déjà « effacé » plusieurs bits (en le divisant par 2, comme indiqué plus haut), et l'entier k indique justement combien de bits ont déjà été « effacés ».
• Étant donné un entier binaire n et un entier k, coder une fonction add_bit : binary -> int -> binary qui calcule le résultat de la somme n+2^k en binaire. Testez-la :

  let () =
    assert (add_bit [0;1;4] 3 = [0;1;3;4]);
    assert (add_bit [0;1;4] 5 = [0;1;4;5]);
    assert (add_bit [0;1;4] 0 = [2;4])
          

• Écrire une fonction add : binary -> binary -> binary qui implémente l'addition générale et la tester sur quelques exemples :

  let () =
    let add_int x y = to_int (add (of_int x) (of_int y)) in
    assert (add_int 19 33 = 52);
    assert (add_int 41 29 = 70);
    assert (add_int 33 85 = 118)
          

Déposer le fichier Binary.ml :

Tas binomiaux

Nous allons maintenant implémenter, dans un nouveau module BinomialHeap, les tas binomiaux. Ce sont des files permettant de stocker efficacement des (multi)ensembles de paires priorité / valeur, d'en ajouter de nouvelles, et d'extraire une valeur de priorité minimale rapidement. L'idée pour stocker n valeurs va être la suivante. Supposons que les indices de bits à 1 dans l'écriture binaire de n soient i₁, i₂, ..., i_k, c'est-à-dire que n = ∑_p=1^k2^i_p. Nous allons découper l'ensemble des valeurs en sous-ensembles de taille 2^i_p, chacun de ces ensembles étant stocké dans les nœuds d'un arbre binomial de rang i_p. Ainsi, un tas binomial sera une liste d'arbres binomiaux de rangs respectifs i₁, i₂, ..., i_k avec i₁ < i₂ < ... < i_p. Autrement dit, un tas binomial est une liste d'arbres binomiaux tels que

1. les arbres de la liste sont des tas (les étiquettes croissent le long des branches),
2. le rang des arbres est strictement croissant dans la liste.

• Définir le type 'a heap des tas binomiaux contenant des valeurs de type 'a.
• Définir une opération add_tree : 'a heap -> 'a tree -> 'a heap qui ajoute un arbre binomial supposé croissant (un tas) à une file. On veillera à maintenir les propriétés précédentes et l'on pourra s'inspirer de la fonction add_bit écrite précédemment.
• Définir une opération insert : 'a heap -> int -> 'a -> 'a heap qui ajoute un nouvel élément de priorité et de valeur données à une file.
• Définir une fonction find_min : 'a heap -> 'a qui renvoie l'élément de priorité minimale le plus ancien d'une file en temps linéaire par rapport au nombre d'arbres. (On ne demande pas ici d'extraire l'élément de la file; seulement de le trouver.) Il pourra être utile d'ajouter au module BinomialTree des fonctions permettant d'obtenir la clé et la valeur de la racine d'un arbre.
• Testez votre implémentation. Par exemple :

  let () =
    let h = empty in
    let h = insert h 5 "a" in
    assert (find_min h = "a");
    let h = insert h 8 "b" in
    assert (find_min h = "a");
    let h = insert h 2 "c" in
    assert (find_min h = "c");
    let h = insert h 2 "d" in
    assert (find_min h = "c");
    let h = insert h 2 "e" in
    assert (find_min h = "c")
          

• Écrivez un fichier d'interface pour ce module.

Déposer les fichier BinomialHeap.ml et BinomialHeap.mli :

BONUS : questions subsidiaires

Les questions suivantes sont optionnelles. Elles permettent de voir l'utilisation que l'on peut faire des files de priorité.

Fonctions auxiliaires sur les files binomiales

Nous allons commencer par implémenter quelques autres fonctions utiles sur les files binomiales.

• Définir une opération merge : 'a heap -> 'a heap -> 'a heap qui fusionne deux files, en vous inspirant de l'addition d'entiers binaires.
• Définir une opération extract_min_tree : 'a heap -> 'a tree * 'a heap qui isole un arbre dont la tête est de priorité minimale dans une file, et renvoie cet arbre, ainsi que la file privée de cet arbre.
• Définir une opération extract_min : 'a heap -> 'a * 'a heap qui extrait d'une file une valeur de priorité minimale de la file. Vérifier que cette fonction a une complexité logarithmique en le nombre d'éléments de la file.
• S'assurer que si la file contient plusieurs valeurs de priorité minimale, la valeur la plus ancienne est renvoyée. Par exemple :

  let () =
    let h = empty in
    let h = insert h 1 "a" in
    let h = insert h 1 "b" in
    assert (fst (extract_min h) = "a");
    let h = insert h 1 "c" in
    assert (fst (extract_min h) = "a")
          

Déposer le fichier BinomialHeap.ml :

Files de priorité

Nous allons finalement utiliser le module des files binomiales pour créer un module PriorityQueue implémentant les files de priorité (de type 'a heap).

• Définir une fonction create : unit -> 'a heap permettant de créer une file de priorité.
• Définir une fonction push : 'a heap -> int -> 'a -> unit qui permet d'ajouter un élément, avec une priorité donnée, à une file.
• Définir une fonction pop : 'a heap -> 'a permettant d'extraire l'élément de priorité minimale le plus ancien dans la file.
• Tester ces fonctions. Par exemple :

  let () =
    let q = create () in
    push q 2 "a";
    push q 1 "b";
    assert (pop q = "b");
    assert (pop q = "a")
          

  et

  let () =
    let q = create () in
    push q 1 "a";
    push q 2 "b";
    assert (pop q = "a");
    assert (pop q = "b")
          

• Définir une fonction is_empty : 'a heap -> bool permettant de déterminer si une file est vide.
• Définir une fonction size : 'a heap -> int déterminant le nombre d'éléments dans une file. Comment l'implémenter avec une complexité logarithmique en le nombre de ces éléments ?

Déposer le fichier PriorityQueue.ml :

Algorithme de Dijkstra

Le module des files de priorité peut être utilisé pour implémenter l'algorithme de Dijkstra qui permet de trouver le plus court chemin dans un graphe dirigé pondéré (chaque arrête est étiquetée par un entier indiquant sa longueur). On trouvera les fonctions de test mentionnées ci-dessous dans le fichier Graph.ml.

• Dans le module précédent modifiez la fonction pop : 'a heap -> int * 'a pour qu'elle revoie la priorité en plus de la valeur.
• Les sommets du graphes seront identifiés par des entiers, et un graphe sera décrit par une liste de triplets indiquant pour chaque arrête sa source, son poids et son but. Celles-ci peuvent être converties sous forme de matrice d'adjacence grâce à la fonction suivante :

  let graph edges =
    let vertices = List.fold_left (fun v (s,d,t) -> max v (max s t)) 0 edges + 1 in
    let g = Array.init vertices (fun _ -> Array.make vertices 0) in
    List.iter (fun (s,d,t) -> g.(s).(t) <- d) edges;
    g
          

• Sur un tel graphe, l'algorithme de Dijkstra permet de calculer le plus court chemin d'une source à un sommet donné. Il peut être implémenté à l'aide de files de priorité de la façon suivante :

  let dijkstra g source =
    let pq = create () in
    let vertices = Array.length g in
    let d = Array.make vertices max_int in
    d.(source) <- 0;
    push pq 0 source;
    while not (is_empty pq) do
      let pi, i = pop pq in
      for j = 0 to vertices - 1 do
        if g.(i).(j) > 0 then
          let dj = d.(i) + g.(i).(j) in
          if dj < d.(j) then begin
            d.(j) <- dj;
            push pq dj j
          end
      done
    done;
    d
          

• Testez cette fonction, par exemple sur le graphe suivant : Le code correspondant :

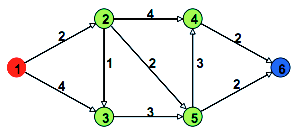
  let () =
    let g =
      graph
        [
          (1,2,2);
          (1,4,3);
          (2,1,3);
          (2,4,4);
          (2,2,5);
          (3,3,5);
          (4,2,6);
          (5,3,4);
          (5,2,6);
        ]
    in
    let d = dijkstra g 1 in
    for i = 0 to Array.length g - 1 do
      Printf.printf "distance to %d : %d\n" i d.(i)
    done
          

  doit afficher le résultat suivant :

  distance to 0 : 4611686018427387903
  distance to 1 : 0
  distance to 2 : 2
  distance to 3 : 3
  distance to 4 : 6
  distance to 5 : 4
  distance to 6 : 6
          

Une solution vous est proposée.