Typestate in Mezzo? Starting with list iterators.
- June 26, 2013
I (Armaël Guéneau) am currently doing an internship with François Pottier, working on Mezzo, which has been introduced by Jonathan in two previous blog posts (the first, the second).
Since the beginning of my internship, I have been playing with Mezzo, writing some code, and, more specifically, trying to see how the notion of typestate could be expressed with Mezzo’s permissions. As an application, I tried to write in Mezzo an iterator on lists. What I call an iterator is here more like Scala’s Iterator , or a bit like what Gabriel called generators in a previous blog post.
This example turned out to be subtle enough to write in Mezzo: in this post, I’ll try to show you the details of the implementation, leading to a fully working implementation of list iterators. I think it’s a good opportunity to see an implementation of a (very simple) typestate, and also some funny tricks with Mezzo’s permissions.
A word of warning, though: while the theory and implementation of Mezzo are starting to fit in nicely, the library-land is very much unknown territory so far. We are trying new things, and expect them to be easier in the future. As always, practice and teaching will surely yield substantial improvements, leading us to see in retrospect how we could have simplified things. Expect the code examples in this post to look complicated, and probably not representative of the Mezzo code we expect to write in the future.
Briefing
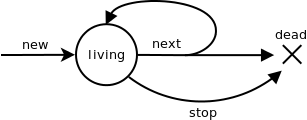
What I want as an iterator is an object that let us iterate on a
collection, giving one new element each time we call a function
next, that makes the iterator go a step forward. Note that
such an iterator is mutable, its internal state being modified by
next. It would be possible to consider functional
iterators, returning a value corresponding to the next position in the
list; but to study the relation with typestate systems we decide to
study mutable iterators here.
We have to handle the case where the iterator has no more elements.
In Java or Scala, you have to check if there are more elements available
with hasNext, and if you call next on an empty
iterator, an exception is raised. In Mezzo we don’t have exceptions.
Moreover, we want to statically express the protocol that the operations
on an iterator must follow, in the types themselves. It’s the idea of
typestate. By achieving that, the user is prevented at compilation
time of using next on an empty iterator.
The application to (simply linked) lists seems straightforward: you
just have to follow the tail link of each Cons
cell, starting with the head of the list. What is not so trivial is how
to express that with Mezzo’s permissions.
The silent iterator
Let’s start with a very stupid iterator: it traverses the list, but without giving its elements to the user.
From the outside: signatures
An iterator has exclusive access on the list
First, to be able to iterate on a list, the iterator will need the
permission to access the list and its contents. A solution is to
consume the permission l @ list a when you
create an iterator on the list l (of elements of type
a), and give it back when the iteration is
finished (or when you stop the iterator manually).
This gives us the following signatures for the new and
stop functions:
val new: [a] (consumes l: list a) -> iterator a (l @ list a)
val stop: [a, post: perm] (consumes iterator a post) -> (| post)In case you’re not familiar with Mezzo syntax yet, you can find more
details in the first
post cited above, but let me just do a quick reminder here. The
bracket notation [post:perm] is parametric polymorphism on
a type of kind perm (a permission), and that
(consumes foo) indicates that type foo is not
given back to the type environment after the functional call. Finally,
(foo | bar) is a conjunction of the type foo
and the permission bar, which may be a purely static
information, not associated to any runtime value; in particular,
(| post) is an empty tuple that is only useful as the
carrier of the permission post.
Expressing iterator typestate
We also need a next function, that takes an iterator in
input. To handle the fact that next may lead to an empty
iterator, we say that next consumes the fact that the input
argument is an iterator, and returns a variant of
option a:
data offer (post: perm) a =
| None {| post }
| Some { x: a }In the first case, the iteration is finished: the post
permission (in practice equal to l @ list a for a given
a and l) is returned. In the second case, an
element is returned. Note that we could have used the sum type of the
standard library, choice a b, but this specific datatype
allows us to give more explicit constructor names (than
Left and Right).
We now have the next signature:
val next: [a, post: perm] (consumes it: iterator a post) ->
offer post (| it @ iterator a post)For now, because our iterator is silent, in the Some
case, we return no value of type a, only the fact that
it is still an iterator, so we can continue the iteration.
On the contrary, after a None answer, it is statically not
possible to call next again: the permission
it @ iterator a post has been consumed and was not returned
through the offer.
A small code example using this iterator:
(* Loop calls [next] on the iterator until it is empty *)
val rec loop [a, post: perm] (consumes it: iterator a post): (| post) =
match next it with
| None -> ()
| Some { x } -> loop it
endDiving into the internals: implementation
A first attempt
To be able to go forward, the iterator must store the elements that
will be explored in the future. With a list, it’s easy: initially, it
consists in the list itself, and each call to next just
takes the tail of the current internal list.
This gives us:
data mutable iterator a (post: perm) = Iterator {
xs: list a
}
data offer (post: perm) a =
| None { | post }
| Some { x: a }
val new [a] (consumes l: list a): iterator a (l @ list a) =
Iterator { xs = l }
val next [a, post: perm] (consumes it: iterator a post):
offer post (| it @ iterator a post) =
match it.xs with
| Nil ->
None
| Cons { head; tail } ->
it.xs <- tail;
Some { x = () }
endSadly, this example doesn’t typecheck: in the match case where
it.xs is Nil, we return None, and
the permission post. However, we don’t have
post!
Formally, at the beginning of next, the only available
permissions are it @ iterator a post, and in the first
match case, it.xs @ Nil. Nothing here gives us
post.
Intuitively, even if we had post at the beginning,
next here doesn’t preserves the knowledge of the cons cells
we have already explored: we have to store in the iterator the
permissions of the previous cons cells, to be able to finally merge them
back into post.
Storing the old permissions
We introduce a new permission, p, that describes the
permission for the consumed cons cells. The iterator contains
p, and a function, rewind, that consumes
p, and the permission on the tail, and merge them into
post.
data mutable iterator a (p: perm) (post: perm) = Iterator {
content: (
xs: list a,
rewind: (| consumes (p * xs @ list a)) -> (| post)
| p
)
}With this definition of iterator, the signature of
next would be:
val next: [a, p: perm, post: perm] (
consumes it: Iterator {
content: (
xs: list a,
rewind: (| consumes (p * xs @ list a)) -> (| post)
| p
)
} ->
offer post (| it @ iterator a (p * xs @ Cons { head: a; tail: unknown }) post)The idea is that before the call to next, the iterator
stores in xs the permission on the non-traversed part of
the list, xs, and rewind requests the
permission on the already-traversed part of the list, represented by
p, upto xs excluded. If xs is
itself a cons cell (and only in this case), we can call
next; the iterator will then store only the tail of
xs, and its rewind function request the permission for
p, plus the first cell of xs – which at this
point as been traversed.
Concretely, imagine we have the following list construction, for some
list lb @ list int.
val la = Cons { head=1; tail=lb }and are now iterating on this list. Assuming we have already called
next once, have traversed the first cell of
la, the rewind function of the iterator would
have a type equivalent to the following:
rewind: (| consumes (
la @ Cons { head:int; tail=lb }
* lb @ list int)
)
-> (| post )If we pattern-match on lb, in the Cons
case, the typing environment will learn that lb has type
Cons { head : int; tail = lc } for some tail
lc @ list int. So rewind has the refined type
rewind: (| consumes (
la @ Cons { head:int; tail=lb }
* lb @ Cons { head:int; tail=lc })
)
-> (| post )The already-traversed part of the list, la, has the same
type, but the not-yet-traversed part has been refined to a cons type.
Note that with the additional hypothesis lc @ int of our
context, this is equivalent to the following type:
rewind: (| consumes (
(la @ Cons { head:int; tail=lb } * lb @ Cons { head:int; tail=lc })
* lc @ list int
)
-> (| post )which is precisely the type of the rewind function of
the iterator returned by next. So after
pattern-matching, the type of the rewind function passed to
next becomes exactly the same as the type of the
rewind function expected as a return value. We can return
this function, unchanged: it has just been transtyped.
val next it (* lengthy type annotation that we won't repeat here *) =
let (xs, rewind) = it.content in
match xs with
| Nil ->
(* p * xs @ list a *)
rewind ();
(* post *)
None
| Cons { head; tail } ->
it.content <- (tail, rewind);
Some
endAs we described, in the Cons case, the value of the
xs field of it is changed to
tail, but the rewind field is unchanged.
Remark: we can still shorten this definition by quantifying
p existentially in the definition of iterator,
and the typechecker will be able to pack and unpack the quantification
to do implicitly what we’ve done explicitly previously (the conversion
p →
p * xs @ Cons { head: a; tail: unknown }).
data mutable iterator a (post: perm) = Iterator {
content: { p: perm } (
xs: list a,
rewind: (| consumes (p * xs @ list a)) -> (| post)
| p
)
}The type for next becomes much more readable. In fact,
it is exactly the one we hoped to get at the very beginning of the
post.
val next [a, post: perm] (consumes it: iterator a post):
offer post (| it @ iterator a post)For the function new, the permission p is
the neutral permission empty, and rewind needs
to do nothing at all:
val new [a] (consumes l: list a): iterator a (l @ list a) =
Iterator { content = (
l,
fun (| consumes l @ list): (| l @ list a) = ()
)}We can also write a stop function that stops the
iteration:
val stop [a, post: perm] (consumes (it: iterator a post)): (| post) =
let _, rewind = it.content in
rewind ()Note that the rewind function never does anything; it is
just used for its effect on the typing environment.
The chatty (and useful) iterator
This is great, we can traverse a list using our iterator. But it would be even more great if we could actually get the contents of the list!
This is a bit more complicated: while giving an element to the user,
we have to give him also the permission on it. This breaks the invariant
“the iterator always can have post by applying
rewind”. Now, our iterator can have a hole in it:
when giving an element to the user, a hole appears. To continue the
iteration, the user must give the permission on the element
back to the iterator.
Consequently, the definition of iterator changes a bit:
an iterator is now also parametrized by a permission
hole, which in fact means “what does the iterator need to
fill its hole and be able to generate post”.
Here is the new definition of iterator. Note that it
doesn’t contains hole, but we need it to generate
post:
data mutable iterator a (hole: perm) (post: perm) = Iterator {
content: { p: perm } (
xs: list a,
rewind: (| p * hole * l @ list a) -> (| post)
| p
)
}Thus, an iterator without a hole is an
iterator a empty post, while an iterator that has given
away x @ a to the user is a
iterator a (x @ a) post.
We can now write next. It takes an iterator parametrized
by any permission hole, the permission hole
itself, and implicitly fills the hole by merging hole into
p. It finally returns the next element (if any).
val next [a, hole: perm, post: perm] (consumes (it: iterator a hole post | hole)):
offer post (x: a | it @ iterator a (x @ a) post) =
let xs, rewind = it.content in
match xs with
| Nil ->
rewind ();
None
| Cons { head; tail } ->
s.content <- tail, rewind
Some { x = head }
endAnd we can now use this iterator:
(* [nth] takes an iterator [it] and an integer [n], makes him go forward of [n]
steps, and then returns it (if it hasn't been consumed) *)
val rec nth [a, hole: perm, post: perm]
(consumes (it: iterator a hole post | hole), n: int):
offer (x: a | it @ iterator a (x @ a) post) post =
match next [hole = hole] it with
| None ->
None
| Some { x } ->
if n <= 0 then (
Some { x = x }
) else (
nth [a = a, hole = (x @ a)] (it, n-1)
)
end You can note that we have sometimes to instantiate by hand the
polymorphic parameters when calling a function. For example, here, when
calling recursively nth, we have to say that a previous
call to next has created a hole of “shape”
x @ a we want to merge back to continue the iteration.
The cherry on top
So, here it is, an iterator on lists!
However, this needs a little cleaning: we store in our iterator a rewind
function, which is the same for every iterator, that doesn’t change over
time, and is just present to convert permissions.
A way to clean up a bit is to declare a toplevel identity function,
named convert:
val convert (): () = ()
alias convertible (p: perm) (q: perm): perm = convert @ (| consumes p) -> (| q)
data mutable iterator a (hole: perm) (post: perm) = Iterator {
content: {p: perm} (
l: list a
| p * convertible (p * hole * l @ list a) post
)
}I find that piece of code cute, and I think it enlightens the way the
transtyping of rewind works: if rewind can have type
(| consumes p) -> (| q) it’s because this is a subtype
of () -> (), which means we have convinced the
typechecker that p is convertible into q.
I want the code!
I doubt so, but just in case, the complete code, with some dummy examples of applications, can be found there.