Fast vectorizable math functions approximations
- January 26, 2015
- Last updated on 2015/01/27
How and why I designed my own approximated implementations of
log, exp, sin and
cos. The approximation error is quite small, and the
functions are fast and vectorizable. For example, my
logapprox function is 7.5x faster in tight loops than the
icsi_log
function, while being more precise.
Recently, I helped my wife optimizing some code doing simulations for her bio-statistics research project. Without going into details, her problem requires doing Bayesian inference using MCMC methods. Those methods are typically very CPU intensive, and in this particular code, most of the time was spent computing logarithms and exponentials. This is a bit disappointing, because the results of these computations are in the end only used as a probability from which we are going to draw a Boolean (they are rejection probabilities of the Metropolis-Hastings algorithm). We are clearly spending a lot of time computing these number with the full double precision, while we need much less.
My first optimization idea was to use an approximated version of the
logarithm and exponential functions. Namely, I used the well-known
icsi_log
function for the logarithm, and I have written a similar function for
exponential. I am going to explain the principle for logarithm:
exponential use similar tricks, but in the other direction. The first
idea is to transform the problem of natural logarithm into base-2
logarithm by multiplying the result by \(\log
2\). Next, recall that
floating-point
numbers are represented by a mantissa and an exponent: using
bitmasks, it is very easy to extract from a normalized floating point
number \(f\) two numbers \(m\) and \(e\) such that \(f
= m2^e\), \(m \in [1,2[\), \(e \in \mathbb{Z}\). Thus, we have \(\log_2 f = \log_2 m + e\), so that we
reduced the problem into computing the logarithm of a number in \([1,2[\), which is done in
icsi_log using precomputed look-up tables.
While the use of these functions brought some speedup, there were two major drawbacks: first, because the look-up table must not be too big (otherwise it will not fit in low-level cache, and look-up would be too slow), the precision is limited. Second, the loops that contained calls to the approximated functions contained accesses to arrays with random indexes, and thus cannot be vectorized.
Loop
vectorization is a technique able to provide huge speedups
(typically x3 at least), when the hottest part of the code is simple
enough. Not-so-old processors have special instructions, called SIMD
instructions, that are able to execute the same operation on several
pieces of data simultaneously. In the x86 world, they are called SSE
instructions. They are typically used when doing repetitive operations
on arrays, and can lead to big speedups. Until recently, if you wanted
your code to be vectorized, you had to manually write code that
explicitly used these features of the processor. This leads to code that
is neither easily maintainable nor portable. However, a lot of progress
had been done, and recent compilers are able to vectorize automatically
simple loops: that is, you write loops as if they were completely
sequential, and the compiler is able to figure out the iterations are
independent, and, when possible, bind them together by using SIMD
instructions. This can lead to huge speedups, and I wanted to take
advantage of this opportunity. Automatic vectorization is enabled in
recent versions of GCC, when using -O3 option. For some
loops, it is necessary to add -unsafe-math-optimizations to
allow GCC to reorder some operations and enable vectorization. The
problem with icsi_log is that accessing tabulated values
cannot be vectorized, and so these functions blocked the automatic
vectorization process of GCC.
I searched for other approximated approximations of these functions: I found Intel’s Approximate Math Library, which is oldish, written in assembly, thus not portable for other platforms, and needed rewriting if used for GCC. Moreover, its use would need manual vectorization, which is not handy.
So, I crafted my own version of log and exp, reusing the trick about the binary representation of floating-point numbers, but replacing the table look-up by a good polynomial approximation. I used the Sollya tool to find those polynomial approximations. Here is, for example, the Sollya script that can be used to find the best polynomial approximation of the natural logarithm in the interval \([1, 2]\) – using the Remez algorithm. It also plots the error :
f = remez(log(x), 4, [1,2]);
plot(f-log(x), [1,2]);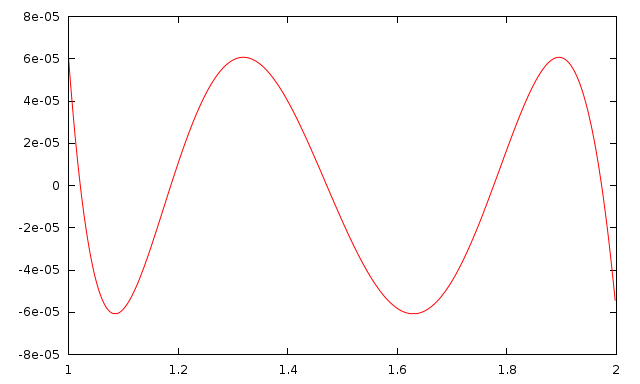
These functions are vectorizable, giving big speedups if used in
appropriate loops. We gain x21 for exponentials (compared to the
expf function in glibc, which does not give much more
precision) and x38 for logarithms (compared to logf
function in glibc, which gives almost twice more correct mantissa bits).
Moreover, their precision is quite good: for exponential, the relative
error is bounded by \(10^{-5}\), and
for logarithm, the absolute error is bounded by \(7.10^{-5}\) (both bounds stand for
“reasonable” inputs are given, that is when denormal numbers are not
involved). That’s better than both tabulated and Intel’s versions.
In the hope it could be useful to someone, I provide the
implementations of both functions, logapprox and
expapprox, with their benchmarking scripts (feel free to
reproduce this), under MIT license: https://github.com/jhjourdan/SIMD-math-prims
I also provide the implementation (sinapprox,
cosapprox) of approximated \(\sin\) and \(\cos\), based on polynomial approximations,
and correct only in \([-\pi, \pi]\),
which represents a common usecase. Future work would be to design
approximations for other common math functions: I’d be happy to
implement or merge your own, if asked for.
Here are the performance results for the logarithm:
Benchmarking logf... 88.9M/s
Benchmarking icsi_log... 470.7M/s
Benchmarking logapprox... 3557.5M/sAnd the accuracy measurements, compared against
logf:
Comparing the behavior of logapprox against logf, in the interval [1e-10, 10]:
Bias: -1.672978e-06
Mean absolute error: 3.756378e-05
Mean square error: 4.211918e-05
Min difference: -6.055832e-05
Max difference: 6.103516e-05For reference, icsi_log, also compared against
logf, is less precise:
Comparing the behavior of icsi_log against logf, in the interval [1e-10, 10]:
Bias: 6.748079e-06
Mean absolute error: 1.771525e-04
Mean square error: 2.089661e-04
Min difference: -4.338026e-04
Max difference: 4.688501e-04